1. Merge Algorithm

sorting된 두개의 배열을 앞에서부터 각각 하나씩 비교하며 한 배열에 순서대로 합치는 알고리즘.
이 알고리즘의 단점은 하나의 배열을 새로 만들어야한다는 것이다
2. Recursive Merge Sort

위 코드를 간단히 설명해보자면
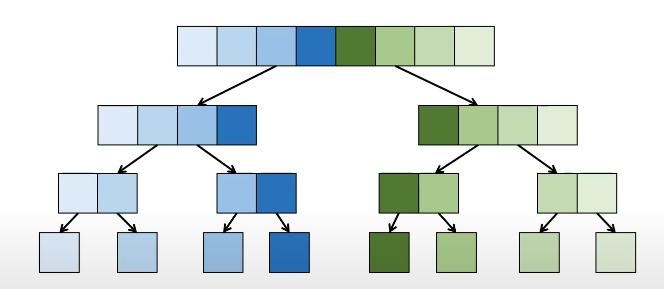
먼저 a[]와 똑같은 b[]를 만든다. h는 배열 전체 길이의 절반이다.
b[0]부터 b[h-1] 까지 sort하는 함수를 한번 호출하고 b[h]부터 b[n-h-1]까지 sort하는 함수 하나를 호출한다.
끝까지 한 다음에는 마지막에 a로 sorting되며 합쳐진다.
증명 (proof by Invariant)
invariant :
조건1 . a 배열이 입력이라고 가정하고 b배열이 sorting된 후 배열이라고 하면, a와 b의 값이 같아야한다.
조건2. 배열 b는 b[0]<b[1]< ... < b[n] 이어야한다. (같은 값은 없다고 가정)
배열을 쪼개고 합치기만 하므로 집합조건을 깰 수 있는 코드는 없다.
증명 (proof by Induction)
위 invariant의 조건2 를 수학적 귀납법으로 증명해볼 것이다.
Base : n=1 이면 return (코드에는 없다)
Step : n/2일 때, Sort()함수가 성공한다면 c[0]<c[1]<...<c[n/2−1] 와
c[n/2]<c[n/2+1]<...<c[n−1] 가 완성된다.
n일 때는 merge 알고리즘의 정확성에 의해
T(n) = n + 2T(n/2)
= n + 2(n/2+2(T(n/4))
= ... = O(nlogn)
'학부 내용 정리 > [ 2-2 ] 알고리즘' 카테고리의 다른 글
| [ 알고리즘 ] MST(1) : Prim Algorithm (0) | 2022.10.11 |
|---|---|
| [ 알고리즘 ] 자료구조 내용 복습 (0) | 2022.10.09 |
| [ 알고리즘 ] 정렬(3) : Quick Sort (0) | 2022.10.09 |
| [ 알고리즘 ] 정렬(1) : Selection Sort, Recursive Selection Sort (1) | 2022.10.09 |
| [ 알고리즘 ] Binary Search, Recursive Binary Search (2) | 2022.10.03 |