반응형
1. Problem Definition
- J1, J2,...,JN 이라고 표기되는 N개의 job이 있다.
- 각 J는 (D,P) 로 쓰이는데, D는 deadline이고 P는Profit 이다.
- 1시간 단위의 타임슬롯이 있고 모든 일은 1시간이 소요된다
ex) (2,2) , (1,3), (1,1)
또, 이 문제는 아래의 가정을 따른다.
- 모든 deadlines은 N이하라고 가정한다. (N보다 크면 N으로 생각해도 됨)
- Job들은 내림차순으로 정렬되어있다.
- Deadline 이후의 일은 안나온다고 가정한다.
직관적으로 보면, 이익이 큰 것부터 최대한 뒤쪽에 배치하는 것이 효율적인 것을 알 수 있다.
최대한 뒤쪽에 두는것이 다른 Job들에게 방해가 될 가능성이 적어보이기 때문이다.
이것도 Greedy 알고리즘이다.
2. Proof of Invariant
Greedy 알고리즘이기 때문에, 앞에서 했던 '알고리즘의 선택이 정답을 벗어나가지 않는다'를 증명하는 방식을 따라간다.
Invariant : i번째 Job Ji를 처리한 직후, 최소한 하나의 optimal solution S 가 존재한다.
S는 다음을 만족한다.
- j ≤ i 인 Jj가 A에 나온다면 S에도 나오고, S에 나온다면 A에도 나온다. A는 알고리즘의 solution이며, S와 A에서의 위치는 동일하다.
Base : i =0일 때, 할일이 없다. 성립한다.
Step: i 번째까지 성립한다고 가정하고, i+1이 성립함을 보일 것이다.
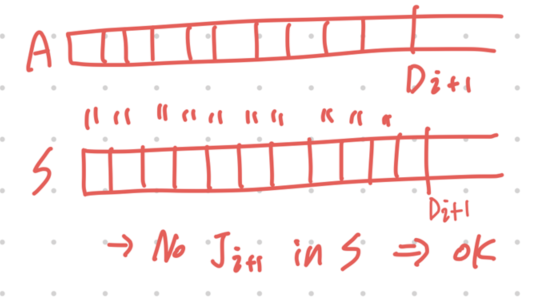
- Case1 : 알고리즘 A가 i+1 번째에 스케줄을 하지 못했다. 이경우는 A에서 Ji+1 의 데드라인 Di+1 이전의 모든 슬랏이 j1부터 jn까지로 가득 차 있는 상태이다. 그러므로 가정에 의해 S에도 j1부터 jn까지로 가득 차 있다. Ji+1은 S에도 없다.
- Case2 : A에서는 Ji+1가 t에 있다.
- Case2.1 : Ji+1가 S에는 없는 경우.
- Case2.1.1 : S에서 t가 비어있을 경우. S에서 t에 Ji+1를 넣는게 더 이득이므로 이 경우는 가정에 모순이 생긴다.
- Case2.1.2 : S에서 t에 다른 Job Jx가 들어있을 경우. Ji까지는 A와 S가 동일하게 배치되어있으므로 x > i+1 일 것이다. x가 더 크다는 의미는 propit이 더 작다는 것이다 ( Px ≤ Pi+1) .그렇다면 Propit이 더 큰 Ji+1로 바꿔도된다.
- Case2.2 : Ji+1가 S에는 다른 곳 t'에 있는 경우
- Case2.2.1 : t' = t 라면 성립한다
- Case2.2.2 : t' > t 인 경우는 불가능하다. t보다 뒤인 곳은 알고리즘이 이미 이미 꽉 채워놓은 상태이기 때문이다.
- Case2.2.3 : t' < t 인 경우에는 swap( t, t' ) 한다. 답은 바뀌겠지만 얻은 propit은 같기 때문에 상관없다.
3. 성능
균형트리를 이용한다면, O(nlogn) 로 가능하다.
- 시작할 때 모든 슬랏을 Insert한다.
- 각 단계에서 Di를 보고 들어갈 자리를 찾는다
- 스케쥴 된다면 트리를 Delete 한다.
4. Another Job Scheculing Problem
4.1 Problem Definition
- J1, J2,...,JN 이라고 표기되는 N개의 job이 있다.
- 각 J는 (S,T) 로 쓰이는데, S는 Start Time이고 T는 End Time이다.
- 두개의 Job은 동시에 실행될 수 없다.
여기서는 어떻게 하면 가장 많이 실행 시킬 수 있을까? 를 본다.
4.2 Solution
- End Time기준으로 Sorting한다.
- 가장 빨리 끝나는 Job들을 쭉 보며 스케쥴링 가능하면 스케쥴링한다. (Greedy)
4.3 Proof
A는 알고리즘이 만들어가는 스케쥴이고 S는 정답이다.
A와 S는 똑같은 위치에 배치되어있다.
만약 A에 있는데 S에 없다면 S∪A - S ∩ A 들 중에서 가장 deadline이 빠른 Job을 추가한다.
반응형
'학부 내용 정리 > [ 2-2 ] 알고리즘' 카테고리의 다른 글
| [ 알고리즘 ] Divide and Conquer : Quick Sort (0) | 2022.10.15 |
|---|---|
| [ 알고리즘 ] Tape Storage (1) | 2022.10.14 |
| [ 알고리즘 ] 최단거리 : Dijkstra Algorithm (0) | 2022.10.12 |
| [ 알고리즘 ] MST(2) : Kruskal Algorithm (0) | 2022.10.11 |
| [ 알고리즘 ] MST(1) : Prim Algorithm (0) | 2022.10.11 |