1. Closest pair
Closest pair은 주어진 점들 중에서 가장 가까운 쌍을 찾는 문제이다.
이 문제는 직관과 심하게 충돌하는 경우가 많다
1차원일 때는 단순하게 sorting 하면 구할 수 있고 2차원일 경우 두 점사이의 거리공식으로 구할 수 있다.
하지만 이 경우에는 O(n^2) 이 필요하다. 이 방법은 어렵지 않다.
우리의 목표는 O(nlogn)이다.
2. Divide and Conquer

먼저 이들을 절반으로 나눈다.
(나누는 것은 x 를 기준으로 sorting 한 뒤 나눠주면 된다)
나눠거 각각 가장 최소거리를 구해준다.
왼쪽의 최소걸이는 DL 오른쪽의 최소거리를 DR이라고 하자.
D = min(DL , DR) 라고 D를 정의하자.

중심 선으로부터 D만큼의 거리에 선을 그으면 위 그림과 같다.
우리는 이 D 안을 밴드라고 부를것이다 (Band)
이 상태에서 오른쪽에서 하나 왼쪽에서 하나를 골라서 비교해보면 D 보다 작은 거리의 점을 찾아낼 수 있다.
선 밖에 있는 점들은 중간선으로 가는 과정이서 이미 D를 넘기 때문에 확인해볼 필요가 없다.
하지만 이 방법을 써도 대부분이 다 D 안에 있다면 비교 하는과정에서 N^2가 나올 수 있다.
2.1 O(nlog^2n)에 푸는 방법
오른쪽, 왼쪽 따로 봤을 때, D 안에 있는 점들의 관계를 보면, 이들은 D보다 가까울 수 없다.
즉, 점을 중심으로 원을 그렸을 때, 원 안에 다른 점은 들어올 수 없다.
이 말은 D 안에 점들이 그렇게 따닥따닥 붙어있을 수 없다는 말이다.
한변의 길이가 D인 정사각형하나에는 점이 최대 3개 들어갈 수 있다.
사긱형이 두개라면 5개까지 될 수 있다.

이렇게 되면 검정색 점은 저 4개의 빨간점끼리만 비교하면된다.
(사각혁 밖은 D가 넘는다)
그렇다면 저 5개 점은 어떻게 찾아야할까?
- 밴드 안의 점들만 모아서 y좌표로 sorting한다.
- 까만점은 자기 위에 5개만 확인한다.
5개만 확인해도 괜찮냐? 하는 질문이 생길 수 있는데,
각 점들은 자기 차례가 있으므로 그 때 체크해 볼 수 있다.
이 과정을 다시 정리해보자면
- 전체 좌표를 x로 sorting해서 개수를 절반 나눈다.
- 왼쪽과 오른쪽에서 각각의 최소거리를 찾는다.
- 그 둘 중 더 작은 거리만큼 경계선으로 떨어진 선을 그린다. (Band 범위설정)
- Band 안 y좌표로 sorting해서 5개씩 비교해본다.
성능은 어떨까?
S(n) = S(n/2) + n + nlogn
S(n/2) : 왼쪽 절반, 오른쪽 절반
n : 점하나당 비교하는 횟수
nlogn : y좌표로 정렬
nlogn 걸리는 일을 logn번 해야하므로 nlogn * logn 이 된다.
즉 O(n(logn)^2) = O(n(log^2n)
2.2 O(nlogn)에 푸는 방법
우리는 밴드 안에 있는것만 y좌표로 sorting했었다.
여기서의 아이디어는 모든 좌표를 y좌표로 sorting 한 뒤 5개씩 band보다 짧은게 있는지 확인하는 것이다.
혹은 밴드 안에 있는것만 따로 모아서 봐도되긴한다.
(추가할당이기 때문에 느려질 수 있음)
이렇게 하는 이유를 보자.
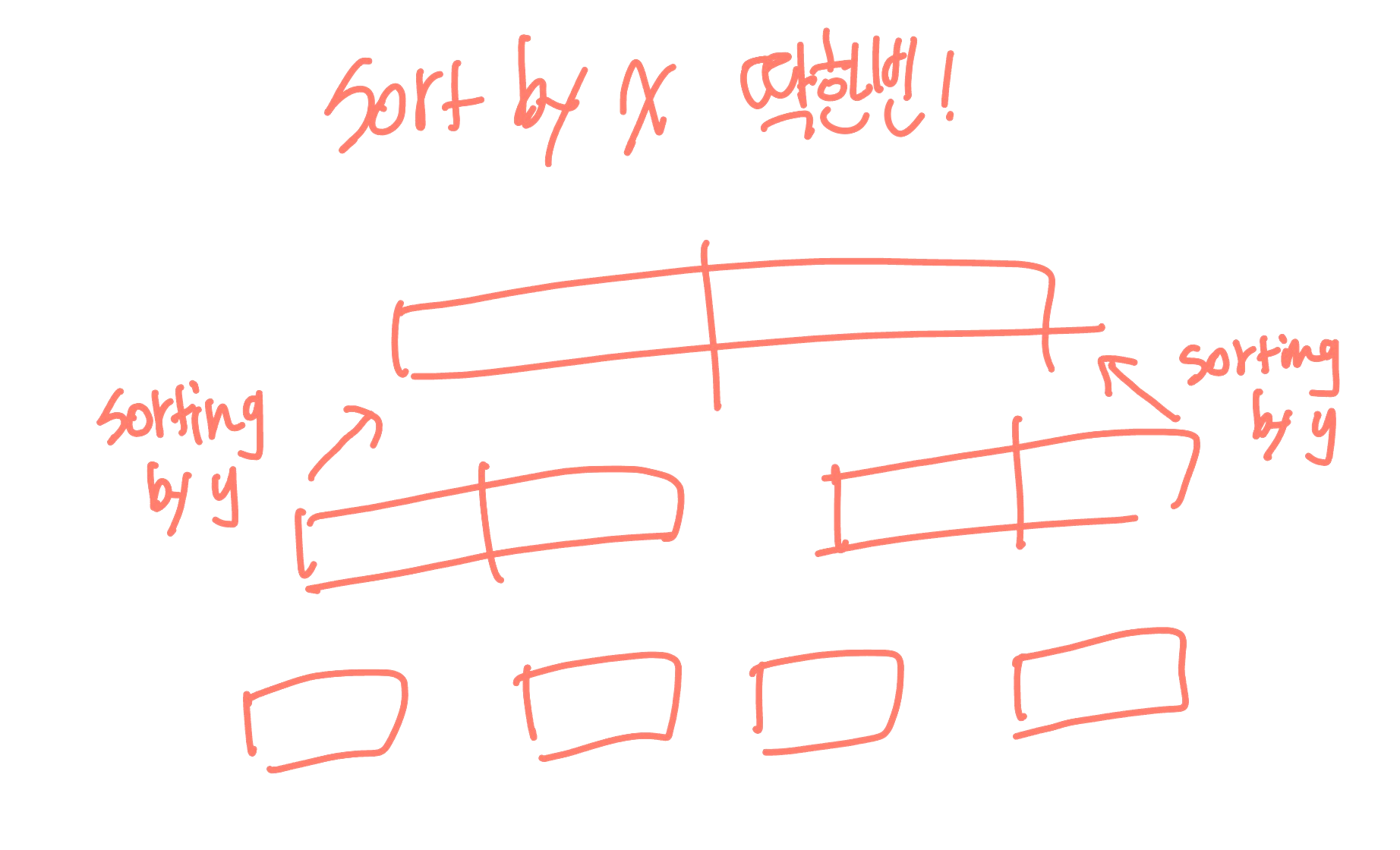
x를 기준으로 sorting하는 것은 맨 처음 딱 한번만이다.
만약 그 이후 밴드 안에 있는 y만 sorting한다면, 나중에 합쳐질때 매번 sorting 해줘야한다.
하지만 전체를 y로 sorting한다면, 나중에 합쳐질 때 merge만 하면된다.
→ O(logn)
시간복잡도를 한번 분석해보자.
S(n) = 2S(n/2) + n +
3. Plane Sweeping
점들을 x 좌표로 sorting 해놓고, 수직선들이 점들을 지나가면서 지금까지 본 것들 중에서 가장 가까운 거리를 수직선에 저장한다. 가장 가까운 거리를 D라고하고 수직선에서 D 사이의 거리를 Band라고 하자.
한 점을 만났을 때, 그 점으로 부터 band 내부의 거리를 y좌표를 기준으로 AVL tree를 만든다.
계속 움직이다가 최소 발견시 D를 update 시킨다.
점을 계속 밀고 나가면서 탈락시켜간다.
→ O(logn)
'학부 내용 정리 > [ 2-2 ] 알고리즘' 카테고리의 다른 글
| [ 알고리즘 ] Matrix Multiplication, Strassen Alg, Karatsuba Alg (0) | 2022.10.18 |
|---|---|
| [ 알고리즘 ] Convex Hull : CCW, Brute-Force-ish, Package Wrapping, Graham Scan, Plane Sweeping, Divide and Conquer, Farthest Point (2) | 2022.10.18 |
| [ 알고리즘 ] Median Problem (0) | 2022.10.17 |
| [ 알고리즘 ] Divide and Conquer : Quick Sort (0) | 2022.10.15 |
| [ 알고리즘 ] Tape Storage (1) | 2022.10.14 |