1. Cut Vertex
Cut Vertex (절단점)는 제거할 경우 그래프가 끊어지게 되는 노드를 의미한다.
각 노드마다 노드를 지우고 그래프가 끊어졌는지를 확인하면 O(n (m+n))의 시간이 걸리게 된다.
하지만 DFS를 돌리고 DFS Tree를 생성하면 O(m+n)만에 절단점을 찾을 수 있다.
1.2. root Cut Vertex
root 노드는 child가 2개 이상이라면 무조건 cut vertex이다.
증명해보자!
1) child가 0개인 경우
루트 노드밖에 없으므로 성립
2) child가 1개인 경우
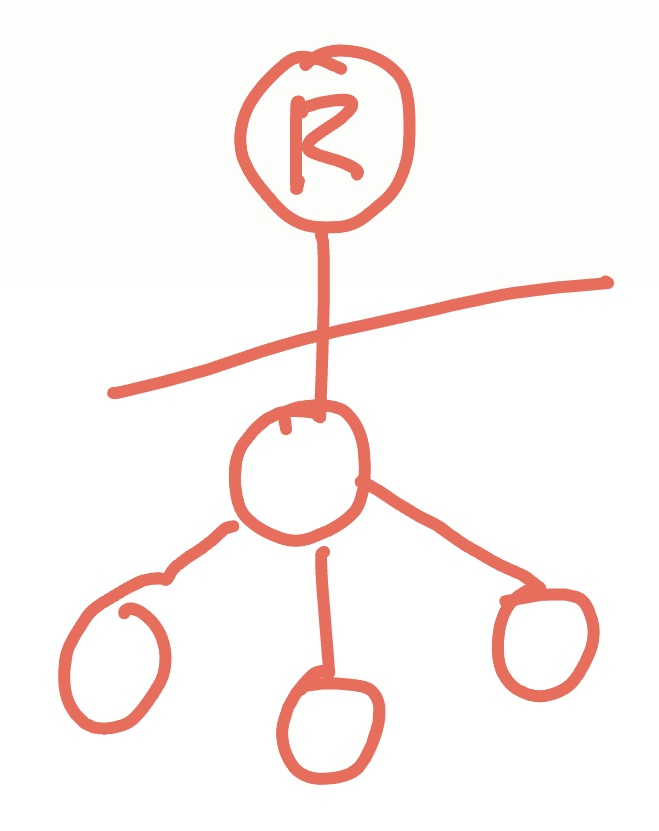
사진과 같이 root노드가 없어도 자식노드들 끼리 다 연결되어있다.
3) child가 2개 이상일 경우
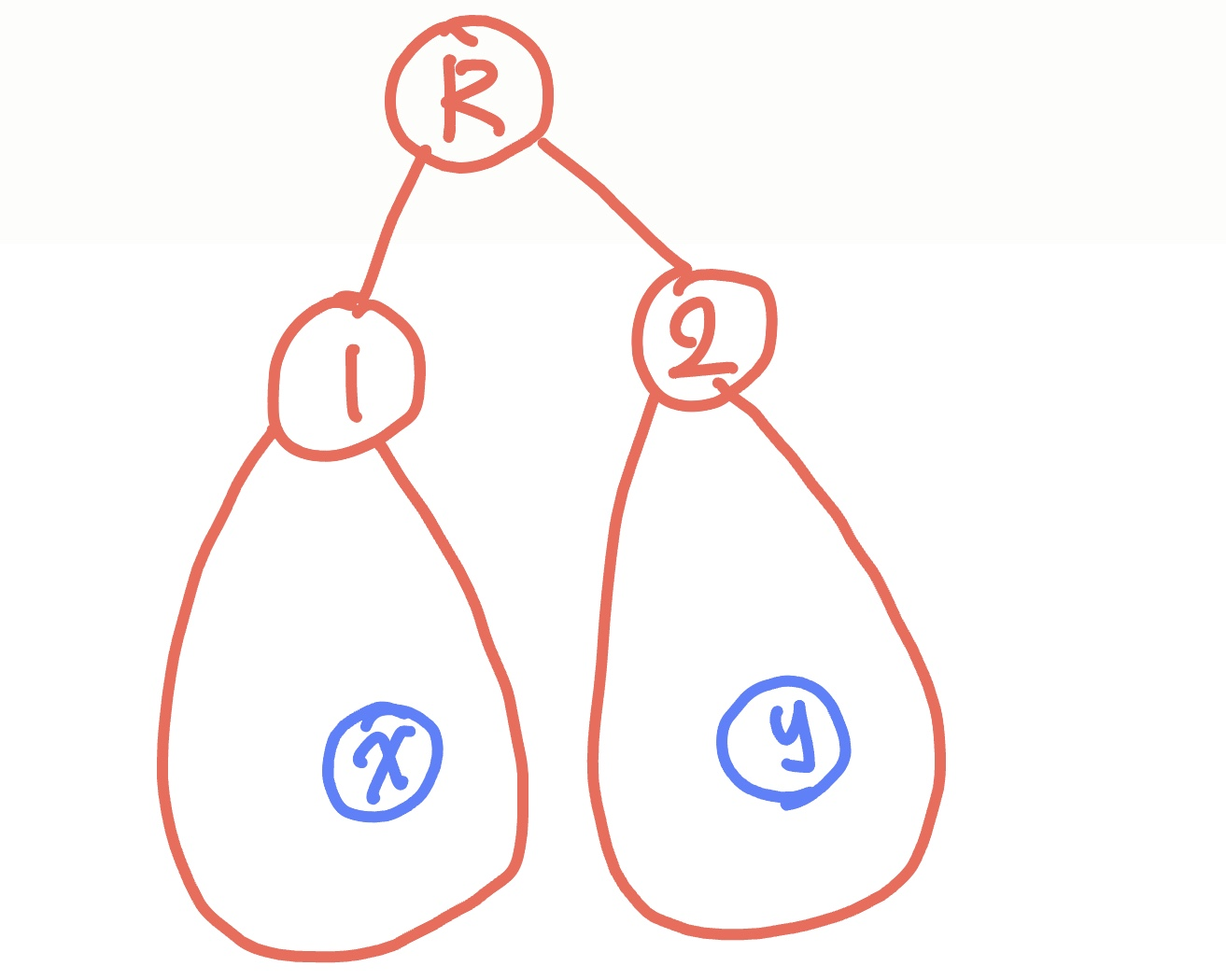
루트노드에 1번 서브트리와 2번 서브트리가 있다고 가정해보자.
1번 서브트리에는 어딘가에 x라는 노드가 있고 2번 서브트리에는 y라는 노드가 있다.
x가 y로 가기 위해서는 1번트리를 벗어나야한다 .
1번 트리를 벗어나기 위해서는 꼭 루트노드를 지나야한다.
back edge를 사용했을 때도, back edge도 결국 조상과 자손을 연결하는 형태이기 떄문에 조상중 가장 높은 root로 가거나, 1번 노드로 갈 것이다. 1번노드로 간다고 해도 꼭 루트노드를 지나야한다.
1.3 Non root cutvertex
DFS Tree에서 루트가 아닌 어떤 노드 t가 Cut Vertex인지 확인하는 알고리즘을 알아보자.
모든 노드마다 (t)를 계산하는데, (t)는 아래 세가지 값들 중 minimum 값을 의미한다.
- Pre(t): DFS 방문 순서 번호 (Pre 번호로 조상-자손 관계만 따질 용도, 위로 갈수록 번호가 작다.)
- t와 연결된 Back Edge의 반대쪽 노드들의 Pre() 값들 중 최솟값 (가장 높은 위치)
- t의 자손들의 l() 값들 중 최솟값
쉽게 말해서, (t)는 의 서브트리 내에서 Back Edge를 한번 타서 올라갈 수 있는 가장 높은 위치의 노드 번호를 의미한다. 노드 t의 자식 u가 존재하고, 이면 가 t의 조상으로 가는 Back Edge가 없는 경우이므로, t는 Cut Vertex이다.
(자식노드들이 올라갈 수 있는 가장 높은 위치가 현재 위치보다 아래에 위치한다는 의미)
Proof
"

back edge를 사용하지 않는경우를 보자. x에서 y로 가기 위해서는 u노드를 거쳐야 u의 서브트리를 벗어날 수 있다. 하지만 u를 거치면 t를 거칠 수 밖에 없다.
back edge를 사용하는 경우를 보자.
"
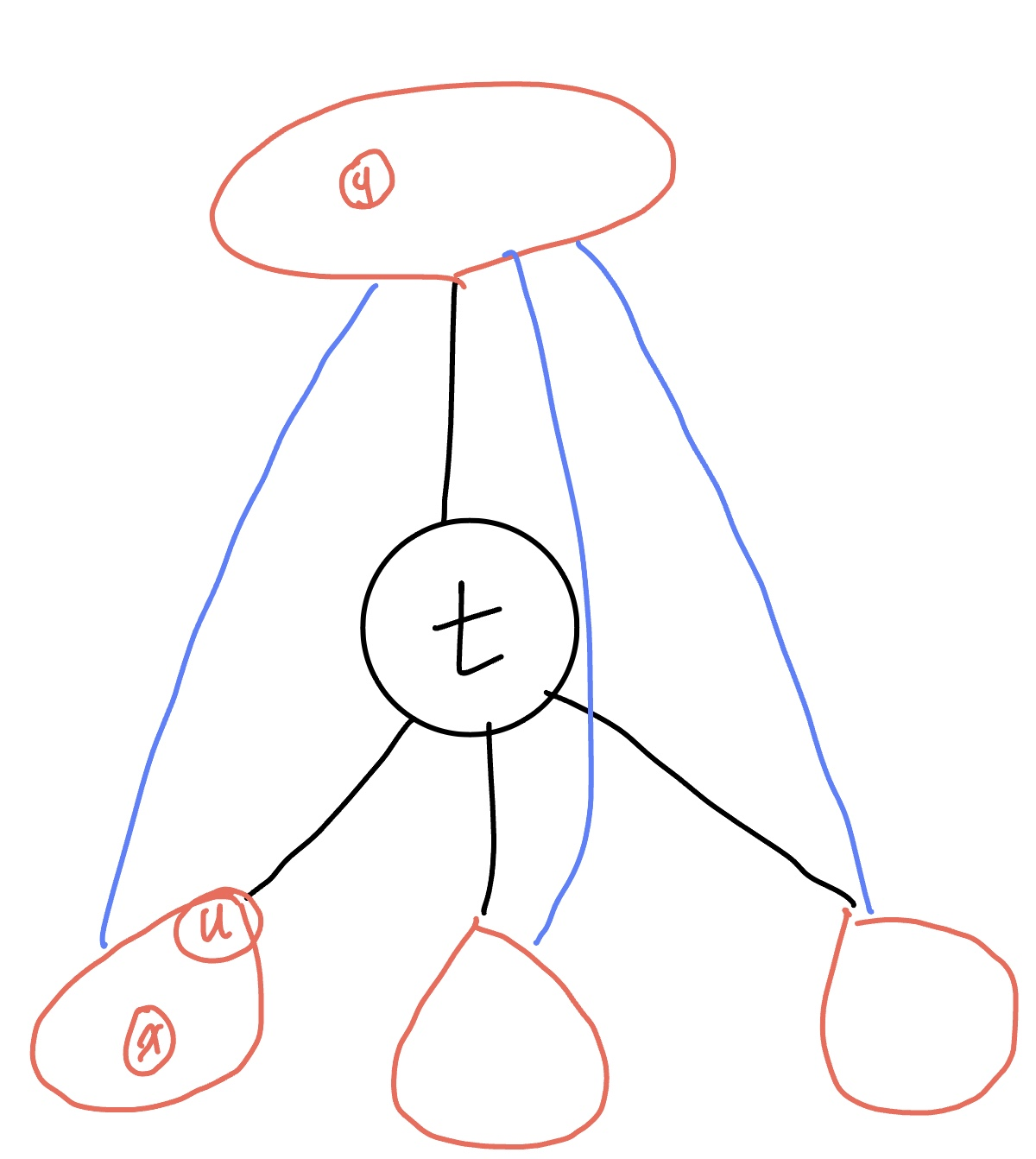
l(u)<Pre(t)이기 때문에 파란색 선과 같은 선이 생길 수 있다.
이렇게되면 x는 굳이 t를 지나지 않고 y로 갈 수 있기 때문에
t는 cut vertex가 아니다.
1.4 시간 복잡도
먼저 처음에 DFS Tree 생성하는데 O(m+n)이 걸린다.
- Pre(t): 처음에 DFS Tree 생성하면서 계산되어 있음
- t와 연결된 Back Edge의 반대쪽 노드들의 Pre() 값들: 금방 계산 가능 (?)
- t의 자손들의 l() 값들 중 최솟값: DFS를 Postorder 순으로 계산해서 한번 더 돌리면 된다.
이 과정에서 DFS를 한번 더 돌리기만 하므로 전체 시간 복잡도는 O(m+n)이다.
2. Biconnected Component
무향 그래프에서 정의되는 개념으로, Cut Vertex에 의해 끊어진 그래프들의 각 부분을 의미한다.
BCC 내의 임의의 두 노드는 완전히 다른 (edge도 node도 겹치지 않는) 2개의 경로만 존재한다.
graph에 cut vertex가 없으면 biconnected이고 이 반대도 성립한다.
2.1 Detecting BCC
BCC를 찾는 방법은 cut vertex를 찾으면된다.
DFS를 하다가 cut vertex에서 멈추면된다.
Cut Vertex 알고리즘에서 아무리 올라가도 노드 t까지밖에 못 가는 Subtree가 있으면 t가 Cut vertex이였다. 이때 이 Subtree가 BCC이다.
3. shortest and longest paths on DAG
topological sort가 된 DAG에서는 Shortest, Longest Path를 찾는 것이 쉬워진다.
간선에 음수가 있어도 구할 수 있다. SSSP 문제는 정렬된 노드 순서대로 다익스트라처럼 가중치를 업데이트 시켜 주면 되고, 입구에서 출구로 가는 SP, LP 문제는 DP와 유사한 방식으로 풀 수 있다.
'학부 내용 정리 > [ 2-2 ] 알고리즘' 카테고리의 다른 글
| [ 알고리즘 ] SCC (Strongly Connected Compnent) (0) | 2022.12.05 |
|---|---|
| [ 알고리즘 ] Topological Sort (0) | 2022.12.05 |
| [ 알고리즘 ] Graph Traversal : Recursive DFS (0) | 2022.12.04 |
| [ 알고리즘 ] Graph Traversal : Any-Order Traversal (0) | 2022.12.04 |
| [ 알고리즘 ] Dynamic Programming : 돌 가져가기, LIS(longest Increasing Subsequence) (0) | 2022.12.01 |