생선 도미와 빙어를 구분하는 머신러닝을 만들어보자!
산점도 그리기
생선 도미의 데이터를 가져와서 산점도로 확인해보자!
파이썬에서 과학계산용 그래프를 그리는 대표적인 패키지는 matplotlib이다.
matplotlib 안에 산점도를 그리는 함수 scatter()함수를 이용하여 도미의 길이와 무게에 대한 산점도를 그려보자!
import matplotlib.pyplot as plt
#도미의 정보
bream_length = [25.4, 26.3, 26.5, 29.0, 29.0, 29.7, 29.7, 30.0, 30.0, 30.7, 31.0, 31.0,
31.5, 32.0, 32.0, 32.0, 33.0, 33.0, 33.5, 33.5, 34.0, 34.0, 34.5, 35.0,
35.0, 35.0, 35.0, 36.0, 36.0, 37.0, 38.5, 38.5, 39.5, 41.0, 41.0]
bream_weight = [242.0, 290.0, 340.0, 363.0, 430.0, 450.0, 500.0, 390.0, 450.0, 500.0, 475.0, 500.0,
500.0, 340.0, 600.0, 600.0, 700.0, 700.0, 610.0, 650.0, 575.0, 685.0, 620.0, 680.0,
700.0, 725.0, 720.0, 714.0, 850.0, 1000.0, 920.0, 955.0, 925.0, 975.0, 950.0]
plt.scatter(bream_length,bream_weight)
plt.xlabel('length')
plt.ylabel('weight')
plt.show()x축은 길이 y축은 무게로 설정하여 산점도를 그리라는 코드이다.
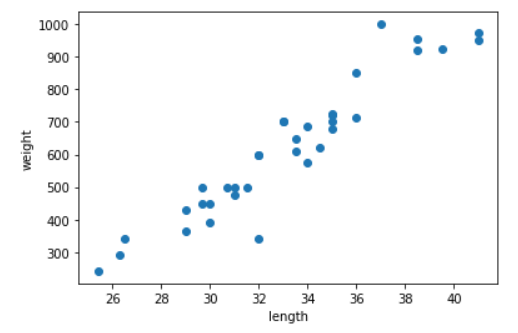
산점도가 잘 나왔다.
그래프를 보니 길이가 길수록 무게가 많이 나간다고 판단할 수 있다.
또, 그래프의 모양이 일직선의 가깝다. 이런 경우를 선형적이라고 한다
두개의 데이터로 산점도 그리기
두개의 데이터로 산점도 그리는 것은 어렵지 않다.
그냥 scatter함수 하나를 더 선언하면 알아서 matplotlib에서 색을 구별하여 보여준다.
import matplotlib.pyplot as plt
#도미의 정보
bream_length = [25.4, 26.3, 26.5, 29.0, 29.0, 29.7, 29.7, 30.0, 30.0, 30.7, 31.0, 31.0,
31.5, 32.0, 32.0, 32.0, 33.0, 33.0, 33.5, 33.5, 34.0, 34.0, 34.5, 35.0,
35.0, 35.0, 35.0, 36.0, 36.0, 37.0, 38.5, 38.5, 39.5, 41.0, 41.0]
bream_weight = [242.0, 290.0, 340.0, 363.0, 430.0, 450.0, 500.0, 390.0, 450.0, 500.0, 475.0, 500.0,
500.0, 340.0, 600.0, 600.0, 700.0, 700.0, 610.0, 650.0, 575.0, 685.0, 620.0, 680.0,
700.0, 725.0, 720.0, 714.0, 850.0, 1000.0, 920.0, 955.0, 925.0, 975.0, 950.0]
#빙어의 정보
smelt_length = [9.8, 10.5, 10.6, 11.0, 11.2, 11.3, 11.8, 11.8, 12.0, 12.2, 12.4, 13.0, 14.3, 15.0]
smelt_weight = [6.7, 7.5, 7.0, 9.7, 9.8, 8.7, 10.0, 9.9, 9.8, 12.2, 13.4, 12.2, 19.7, 19.9]
plt.scatter(bream_length,bream_weight)
plt.scatter(smelt_length,smelt_weight)
plt.xlabel('length')
plt.ylabel('weight')
plt.show()빙어의 데이터를 주가해주고 scatter함수를 빙어의데이터로 실행시키면 결과가 잘 나온다.
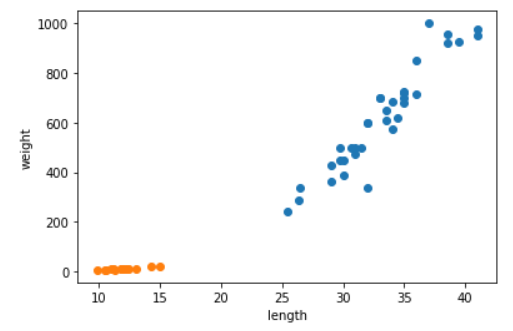
주황색 점이 빙어의 산점도이다.
도미의 비해 길이도 무게도 많이 적다는 것을 알 수 있다.
또, 선형이지만 길이에 따라 무게가 많이 안변한다.
k-최근접 알고리즘
k-최근접 알고리즘은 데이터의 답을 구할 때 주위의 다른 데이터를 중 다수를 차지하는 것을 정답으로 하는 알고리즘이다.
k-최근접 알고리즘을 위해 일단 두 리스트를 합쳐 하나의 길이와 무게 리스트로 만들자.
length = bream_length+smelt_length
weight= bream_weight+smelt_weight머신러닝 패키지 사이킷런을 사용할 것인데 이 것을 이용하기 위해서는 [길이, 무게] 로 이루어져있는 2차원리스트가 필요하다.
지금 우리가 가지고 있는 배열로 사이킷런이 원하는 모양을 만드려면 zip()함수와 for문을 사용하면 된다.
zip()함수는 나열된 리스트에서 각각 하나씩 원소를 꺼내 반환하는 함수이다.
fish_data = [[l,w] for l,w in zip(length, weight)]이제는 각 데이터들의 정답을 알려줘야한다.
도미는 1, 빙어는 0이라고 하자.
도미와 빙어를 순서대로 나열했기에 정답리스트는 순서대로 1이 35개 0이 14개가 될 것이다.
fish_target=[1]*35 + [0]*14이제 대망의 k-최근접 이웃 알고리즘 클래스 KNeighborsClassifier를 사용해보자
from구문으로 import해주자. from은 패키지나 모듈 전체는 import하지 않고 특정 클래스만 import 하는 방법이다.
그렇게 되면 클래스를 사용할 때 패키지 이름을 말하지 않아도 돼서 간편하다!
이후 객체를 만들어 훈련을 시켜보자.
훈련이란 모델에 데이터를 전달하여 규칙을 학습시키는 것을 의미한다.
사이킷런에서는 fit()함수가 훈련을 이 역할을 담당한다.
우리는 함수에게 생선의 데이터와 정답리스트를 주면 된다.
이제는 얼마나 잘 훈련됐는지를 확인해야한다.
사이킷런에서 모델을 평가하는 함수는 score()함수이다.
이 함수는 0에서 1사이의 값을 반환하고 1은 모든 데이터를 정확하게 맞혔다는 의미이다.
이를 정확도(accurancy)라고 부른다!
from sklearn.neighbors import KNeighborsClassifier
kn=KNeighborsClassifier()
kn.fit(fish_data,fish_target)
kn.score(fish_data,fish_target)코드를 돌려보면 실제로 1.0이 나온다!
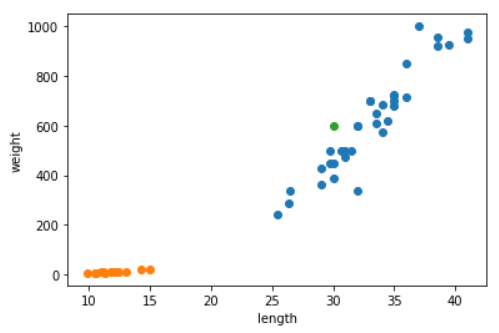
만약 위 그래프에서 초록색 점은 k근접 알고리즘이 무엇이라고 판단할까?
주위에 있는것들이 모두 파랑, 즉 도미이므로 도미라고 예측할 것 같다.
사이킷런에서 predict()함수는 새로운 데이터의 정답을 예측한다.
저 초록색 점의 데이터인 길이30 무게600을 함수에 넣어보자.
kn.predict([[30,600]]) #인자가 2차원 리스트이렇게 넣으면 함수는 1, 즉 도미라는 결과를 낸다.
k-최근접 알고리즘 원리
이 알고리즘은 가장 가까운 직선거리에 데이터들이 어떤 데이터인가를 보고 정답을 판단한다.
그렇기 때문에 입력데이터가 많으면 모든 데이터들과 직선거리를 구해야하므로 이때는 사용하기 힘들다.
또, 보통 사이킷런의 KNeighborsClassifier은 가까운데이터 5개를 보고 정답을 판단한다.
이는 객체를 선언할 때 매개변수로 >> n_neighbors=숫자<<를 넣어주면 된다.
이 숫자를 결정하는 것도 매우 중요한 일이다.
지금 우리가 가지고있는 생선의 개수는 총 49개이다.
이때 매개변수로 n_neighbors=49로 설정해준다면 49개의데이터중 다수를 차지하는 것을 정답으로 처리하므로
도미가 더 많은 우리 데이터에서는 모든 점이 다 도미라고 판단되게 될 것이다.
'공부 > 머신러닝' 카테고리의 다른 글
| [ 머신러닝 프로그램 ] 선형 회귀 알고리즘, 다항 회귀 알고리즘 (0) | 2023.02.17 |
|---|---|
| [ 머신러닝 프로그램 ] k최근접 이웃 회귀 알고리즘 (0) | 2023.02.13 |
| [ 머신러닝 프로그램 ] k-최근접 이웃 분류 알고리즘 ver3 - 데이터 전처리 (0) | 2023.02.13 |
| [ 머신러닝 프로그램 ] k-최근접 이웃 분류 알고리즘 ver2 - 테스트 세트 추가 (0) | 2023.02.11 |