반응형
우선 Merge Sort에 대해 알아 보기 전에 Merge에 대해 알아보자.
Merge 와 Merge Sort 는 서로 같은 뜻 같지만 실제로는 둘이 조금 다르다.
Merge 알고리즘은 soring 된 배열 두개를 합쳐서 새로운 배열을 만드는 알고리즘이다.
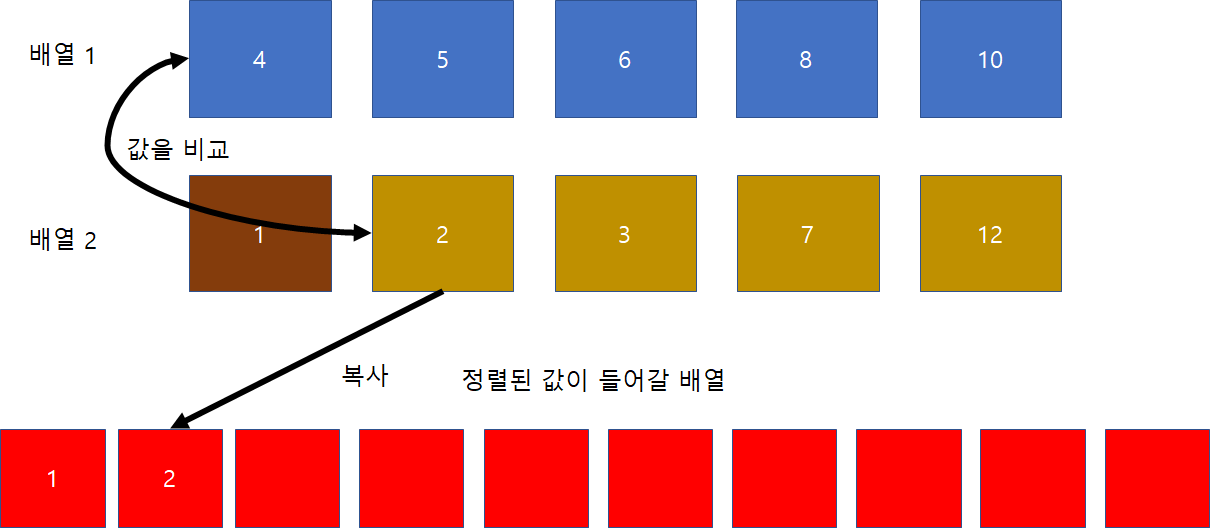
두 배열을 앞에서부터 비교해 나가면서 작은것들을 복사해서 한 배열에 넣는 알고리즘이다.
이러한 알고리즘을 이용하는 것이 Merge Sort 이다.
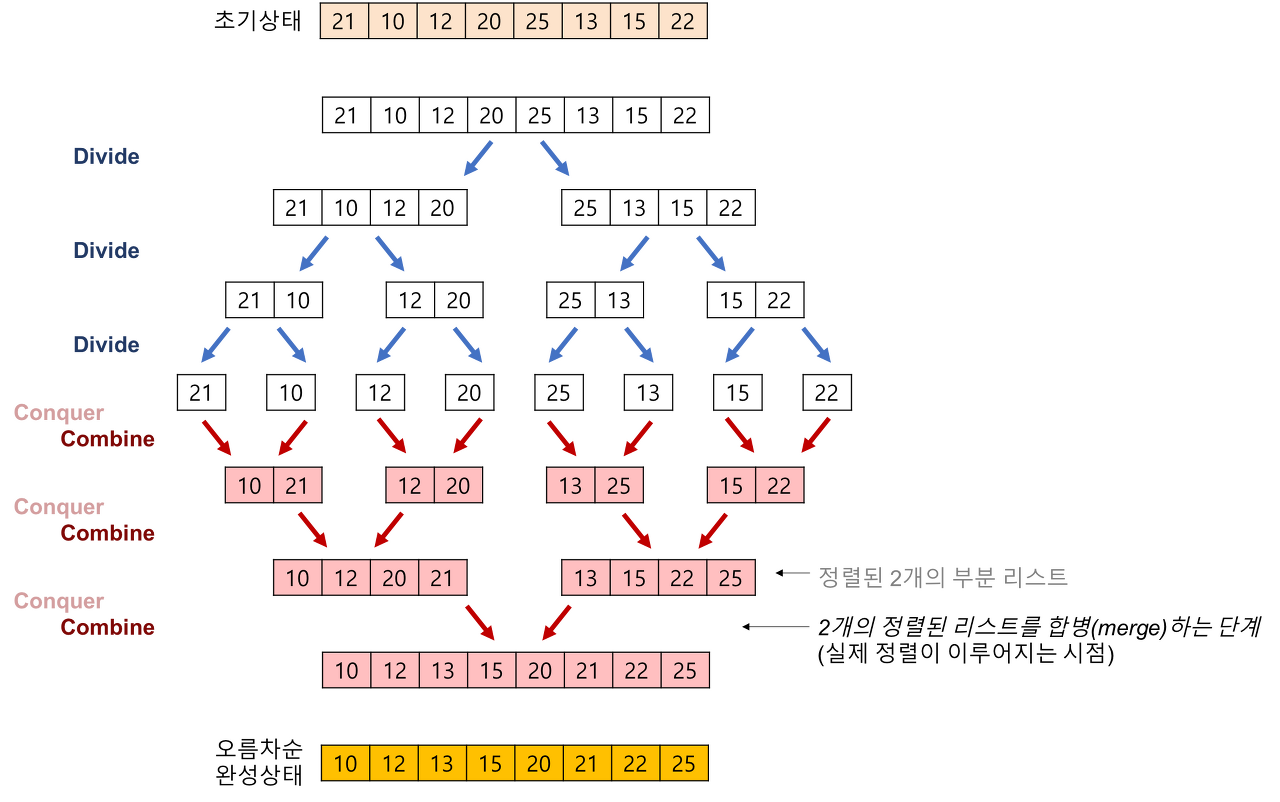
어떤 배열을 나눈다음에 서로 2그룹씩 합치면서 점점 올라오면서 정렬하는 것이 Merge Sort의 기본적인 로직이다.
int sort(int a[], int n)
{
int h;
int b[n];
h = n / 2;
// copy a[] to b[]
sort(b,h); // 반 나눈거의 앞부분
sort(b+h,n-h); // 반 나눈거의 뒷 부분
//Merge two halves in b to a (생략)
return;
}Proof by Induction
- 집합 조건을 깰 수 있는 코드는 지금도 없음.
- Base : n =1 . 할일이 없음
- Step:
- n/2 일 때 sort()함수가 성공한다면 (짝수)
- => 즉, 재귀 호출이 끝난 후 a[0] < a[2] < .... <a[n/2-1] and a[n/2]<a[n/2+1]< ... <a[n-1] 이라면
- n일때 sort()함수가 성공한다.
- => 함수가 끝날떄 a[0]<a[1]<a[2] < ... < a[n-1] 성립
집합 조건을 깰 수 있는 코드는 없다. 코드를 보면 merge도 그렇고 배열 원소의 복사와 이동만 하기 때문에 전체적은 집합을 깰만한 조건은 보이지 않는다.
n/2 일때 (짝수라고 생각) sort() 함수가 성공한다면 두개의 배열로 나눈 배열은 sorting 이 되어있는 상태다.
n일 때 sort 함수가 성공하는가? n/2 일때 성공한 두개의 배열을 결국 merge를 하고 합쳐서 a로 복사하게 된다
그래서 a[0]<a[1]<a[2] < ... < a[n-1] 이 성립하게 된다. merge의 정확성은 이미 알고 있으므로 따라서 정확하다고
설명할 수 있다.
The Complexity
T(n) = n+ 2T(n/2)
= n + 2(n/2 + 2T(n/4))
= n + 2(n/2 + 2T(n/4+2T(n/8)))
= ... = nlogn
따라서 T(n) = O(nlogn)
반응형
'학부 내용 정리 > [ 2-1 ] 자료구조' 카테고리의 다른 글
| [ 자료구조 ] String Matching (Naive , DFA , KMP) (0) | 2022.06.13 |
|---|---|
| [ 자료구조 ] 배열 (Search, Insert, Delete) (0) | 2022.06.13 |
| [ 자료구조 ] 배열 (Selection Sort, Recursive Selection Sort) (0) | 2022.06.13 |
| [ 자료구조 ] 배열 ( Binary Search, Recursive Binary Search) (0) | 2022.06.13 |
| [ 자료구조 ] 기본사항: 수학적 귀납법, 시간복잡도 (0) | 2022.06.13 |