Problem Defintion
- Text : 간단한 문자열
- Pattern: 간단한 문자열
- To Do : 패턴을 발생하는 곳 찾기
Text : abababcabcabcdabccbaabdabcabcdabcd
다음과 같은 text에서 abcabcd 를 찾는 문제라고 생각해보자.
사람이라면 한글자 한글자 보겠지만 굉장히 느린방법이고 사람중심적인 방법이다.
1) Naive 알고리즘
Naive 알고리즘은 아까 위에서 설명한 사람이 한 것과 같은 방식의 알고리즘이다.
사람이 할때는 패턴을 하나씩 옮겼지만 컴퓨터로 이를 구현할때 어떻게 표현해야 할까?
코드로 표현하면 다음과 같다.
// n 은 문자열의 길이
// m은 패턴의 길이, output은 결과
int naivematch ( char T[], int n, char P[], int m, int output[] )
{
int i, j;
for (i = 1; i<=n; i++) output[i] =0 // 아웃풋 초기화
for( i=0 ; i < n ; i++ ){
j=0;
while(T[i+j]==p[j]){
output[i+j]= max(output[i+j],j+1);
j++
}
}
}i가 텍스트의 인덱스, j 패턴의 인덱스이다.
output에는 각 인덱스 번 째에 있는 문자열이 그 패턴의 문자열과 몇번째 같은 문자열인지에 대한 내용이 적혀 있다.
while문을 보면 텍스트의 앞글자부터 한칸씩 이동하면서 패턴과 같은지 확인한다 .
같으면 지금 몇번째 패턴까지 확인했는지와 이미 output에 들어있는 숫자와 비교하여 더 큰 숫자를 output에 넣게 된다.
그럼 output에는 가장 많이 겹쳤을 때 몇번째 겹치는건지에 대한 숫자가 들어갈 것이다.
시간은 얼마나 걸리게 될까? 대략적으로 텍스트길이 n 과 패턴길이 m을 곱한 O(nm) 이 될것이다.
공간은 어찌되었든 텍스트 길이 n에서 움직이므로 O(n) 정도 나올것이다.

2) DFA 알고리즘
DFA 알고리즘은 위의 문제에서 정해진 약속대로 숫자를 적어 패턴을 찾아내는 알고리즘이다.

abcabcd 패턴을 이런식으로 숫자를 활용해 패턴을 찾아 내는 것이다. 이 숫자는 무슨 의미일까? 자세히 설명을 하겠다.
컴퓨터에서는 이런방식을 활용하기 위해 다음과 같은 테이블을 활용하게 된다.
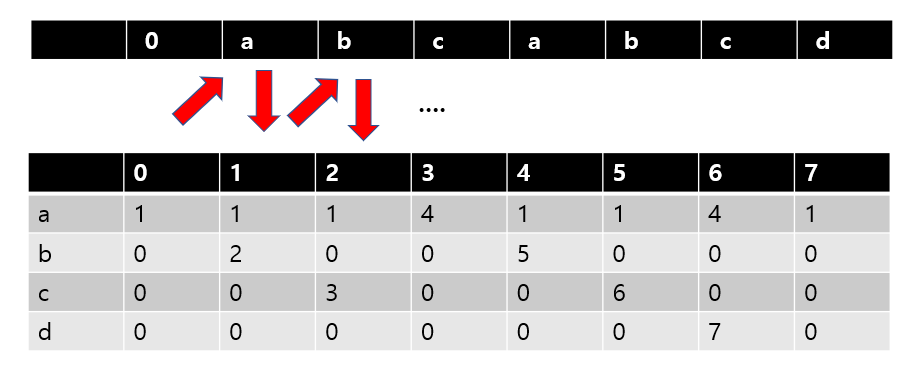
위 테이블은 여러가지 경우에 대해서 어떻게 해야할지에 대해 나와있는 테이블이다.
0이 있는 세로줄을 보면 a에 1이라고 되어있다. 그 말은 즉은 맨처음에 a를 만나면 1번 칸으로 가라 라는 의미가된다.
1번 세로줄을 보면 a를 보면 다시 패턴을 시작하도록 1번으로 가라 라고 되어있고 b를 만나면 두번째까지 일치한 것이니 2으로 가라 라고 되어있다.
2번 줄을 보면 a를 만나면 다시 패턴을 시작하도록 1번으로 돌아가고 c를 만나면 3번으로 가라고 되어있다.
3번 줄을 보면 a 를 만나면 패턴에 맞음으로 다음 줄을 보라는 의미이다.
코드로 짜면 대강 이런 형식으로 나오게 된다.
int table[4][8] = {(1,1,1,4,1,1,4,1),
{.......;
int DFmatch (char T[], int n, int output[]) // 찾고자하는 문자열, 길이, 결과배열
{
int i;
i = 0; s = 0;
for (i =1; i<=n; i++){
s = Table[T[i]-'a'][s]; // text 글자를 a=0 b=1 c=2 d=3 으로 바꿈
output[i]=s;
}
}
이 알고리즘의 공간과 시간은 얼마나 될까? 보통 우리가 쓰는 알파벳을 시그마(∑ = alphabet)로 표시를 한다.
공간은 테이블의 크기와 같으므로 O(|∑|m) (알파벳사용 갯수 * 패턴 크기) 이라고 생각하면 된다.
시간은 O(|∑|m+n) 이다.
테이블을 만드는 것은 다행히 만들어주는 알고리즘이 있고, 루프를 n까지 돌기 때문에 다음과 같이 나오게 된다.

2) KMP 알고리즘
KMP 알고리즘은 DFA와 비슷하면서도 조금 더 메모리를 적게 먹는 알고리즘이다.
전반적인 과정은 비슷하지만 텍스트와 패턴을 비교했을때 다른 글자가 나올경우 다른 방법으로 처리하게 된다.
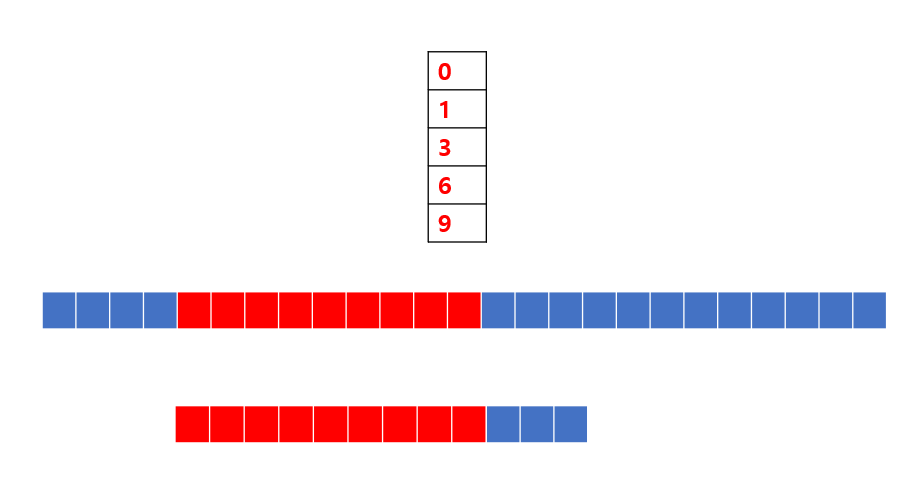
위에가 text 밑에를 pattern이라고 하자. 그리고 위의 숫자가 써있는 표가 있다. 이것의 용도를 차차 설명하겠다.
일단 상황을 하나 가정하자 텍스트에 값들이 써져있다고 생각한다. 아래의 사진을 보자

9번째 까지 문자열이 같음을 확인했고 다음 문자열도 같다면 10을 적고 다음 문자열을 확인할 것이다.
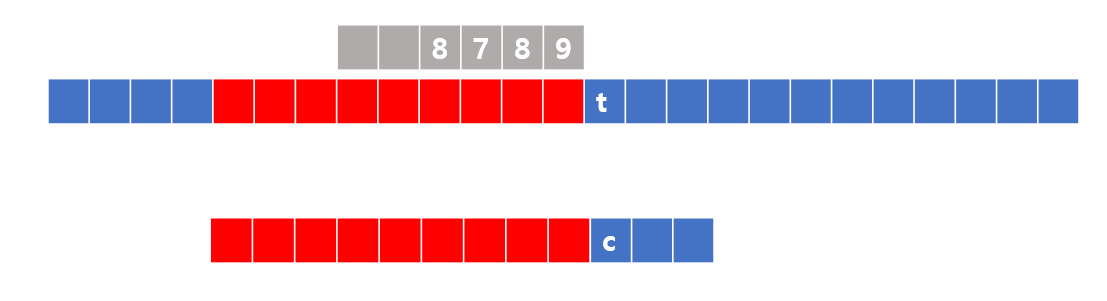
하지만 위 사진은 9번째까지는 같았지만 10번째가 다르다.
이렇게 되면 DFA같은 경우에는 만들어진 Table을 보고 적을 숫자를 결정한다. 만약 t가 패턴의 빨간 부분어딘가에 존재한다면 숫자를 적고 그곳에서 부터 다시 비교작업이 들어가기 시작한다.
그러나 KMP알고리즘은 이를 해결하기 위해 맨 처음 사진의 빨간색으로 쓰여진 배열을 쓴다.
위의 숫자는 패턴이 가지고 있는 성질을 이용한 숫자들이다. 먼저 9라고 써있는게 무슨뜻인지 다시 한번 생각해보자.
지금 까지 그 전에 본 9번째 글자까지 패턴과 텍스트가 일치했다는 의미이다. 그러면 저 위에 숫자는 무엇을 적어놓은 것인가? 9번째가 일치하기전에 패턴과 일부분 일치한 부분이 있을것이다.
따라서 맨 위의 숫자들은 각각 아래 그림과 같은 뜻이 된다.
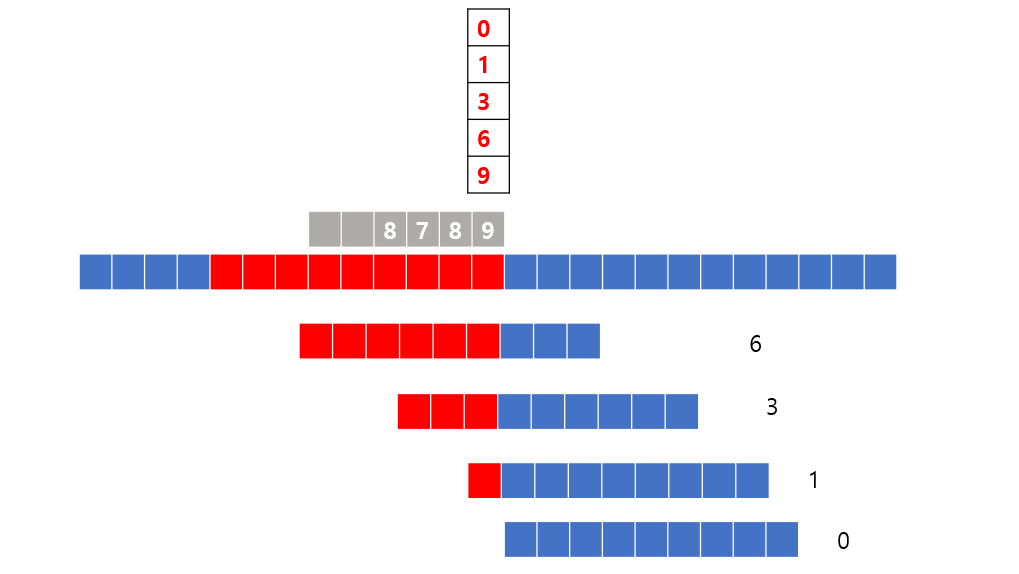
그렇다면 9다음 글자가 틀렸을 때 kmp 알고리즘 은 어떻게 하겠는가? 9다음 6이라고 써 있으니 6을 가지고 와서 그다음값이 7인지 확인을 하는 과정을 가질 것이다. 3보다 6이 더 많이 맞아있기 때문에 9다음 제일 긴 6을 가지고 시도를한다.
그렇게 계속 다를경우 그다음 케이스로 넘어 간다. 이런식으로 패턴을 하나하나 순서대로 맞춰나아가는 것이 kmp의 흐름이다. 결국 맨위의 숫자는 패턴의 특징을 적어놓은 것이라고 할 수 있다.
그럼 이것을 어떤식으로 적어놔야 할까? 9에는 6이 써있고, 6에 3이 가지고 있기 때문이다. 마지막 인덱스에는 -1를 적어 놓는다.
그래서 우리는 이를 바탕으로 Failure Function을 정의할 수 있다.
Failure Function
- Pattern의 P의 앞부분 k글자까지 매치되었을 때 다음 번 시도할 Pattern 앞 부분의 길이
그러면 이제 코드로 KMP 알고리즘의 흐름을 살펴 보자.
KMP Code
int f [8] = {-1, 0, 1, 1, 2, 2, 3, 4, 5, 6, 8, 4, 1};
int KMPmatch(char T[], int n, int output[])
{
int i, s; //시도중인 인덱스, 매치된 글자
i = 1; s = 0;
while(i<=n) {
if(P[s+1]==T[i]){ // 다음께맞았을 때
output[i]=s+1; i++; s++;
}else{ // 다음께 달랐을 때
if(s==0){output[i]=0; i++;} // f[] 시도 다 해봣는데 다 안됨, 0입력
else{s = f[s]; } // 매치 된 숫자 변경하고 재시도, i 변화 없음
}
}
}
}이 코드에는 빼먹은 과정이 있다. s를 증가시키면 안되는 경우가 있다. 답을 찾게 되고나서 또 다시 돌아야 하는 경우
다시 밀어 두어야 하는 과정이 빠진 코드이다.
이제 KMP의 시간 복잡도와 공간 복잡도를 알아보자. DFA와 다르게 매번 루프를 돌때마다 i 가 더해지지 않기 때문에 (같은 값을 계속해서 보는 과정이 있기 때문에) 시간 복잡도를 계산하기 조금 이상해(?)진다.
일단 케이스가 3가지가 있다. 실패한 경우, 성공한 경우, 성공도 실패도 아닌 경우 이렇게 3가지이다.
각각 X, O, R 이라고 하자.
이렇게 한번 쫙 도는게 아니라 어떨때는 다시 멈춰서 보고 하는 경우가 종종 있다.
이럴 때는 우리는 Amortized Analysis 라고 부른다.
Amortized Analysis
- 루프 마다 실행 시간이 다름
- 계산 1 : (루프횟수) X (가장 오래 걸리는 경우의 시간)
- 계산 2 : 각 루프의 실행 시간을 모두 따져서 더한다.(계산 1로 계산하기 어려울 때)
이 경우 우리는 계산2를 쓸 수 밖에 없다. 계산1을 활용하면 결국 O(n^2)이 되기 때문이다.
그러면 우리는 어떻게 계산2를 활용해서 시간복잡도를 계산해야할까?
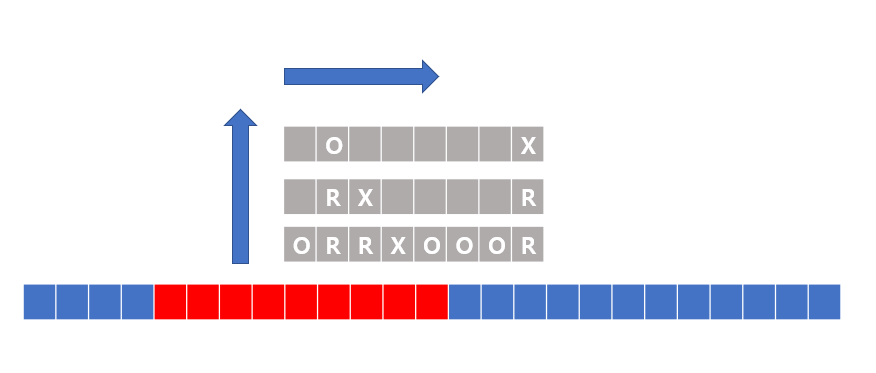
다음과 같이 예시를 생각해보자. 여기서 보면 O의 개수와 X의 개수를 더하면 N의 개수가 되는 것을 알수 있다.
그렇담 유일하게 궁금한것은 R의 개수이다. R이 일어 날때 무슨일이 일어 나는지 생각해보자. R를 할때마다 반드시 패턴이 옆으로 움직이게 된다.(겹치는 개수가 바꾸기 때문에) 그러면 이걸로 R의 개수를 어떻게 제한할 수 있나? 패턴이 옆으로 가는 것은 한계가 있다. 앞서 우리가 본것처럼 R은 절대 패턴의 길이보다 많아 질수는 없다. 패턴이 옆으로 끝까지 밀리면 끝이나기 때문이다. 따라서 R은 개수는 N보다 작거나 같다. 따라서 O,X,R은 O(n) 이다.
이제 Failure Function을 만드는 시간을 알아보자. 놀랍게도 이과정은 텍스트에서 매칭하는 과정하고 같게 된다. 따라서
Failure Function을 만드는 시간은 O(m) 이 된다. 결과적으로 정리하면 다음 표와 같다.

'학부 내용 정리 > [ 2-1 ] 자료구조' 카테고리의 다른 글
| [ 자료구조 ] Queue (0) | 2022.06.14 |
|---|---|
| [ 자료구조 ] Stack (0) | 2022.06.14 |
| [ 자료구조 ] 배열 (Search, Insert, Delete) (0) | 2022.06.13 |
| [ 자료구조 ] 배열 (Merge, Recursive Merge Sort) (0) | 2022.06.13 |
| [ 자료구조 ] 배열 (Selection Sort, Recursive Selection Sort) (0) | 2022.06.13 |