Queue
- Insert/Delete만 제공
- First in, First out( 먼저 들어오는게, 먼저 나가는 것)
- 성능: Insert O(1) , Delete O(1)
Queue 구현
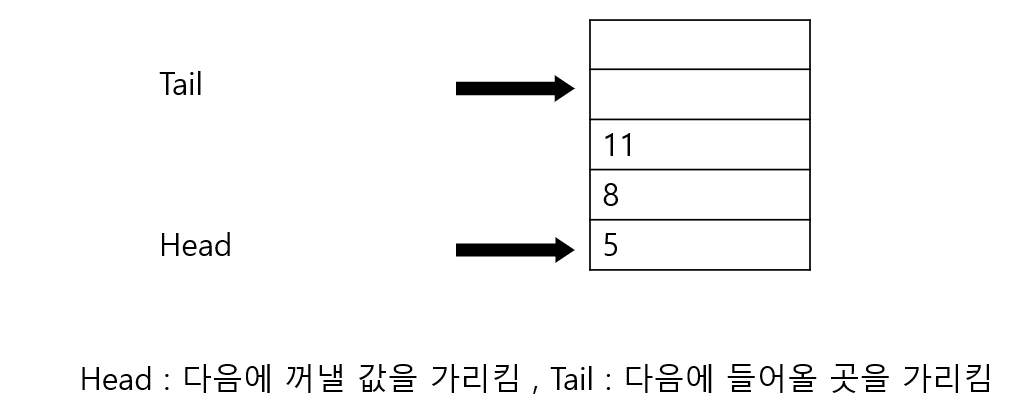
Stack과 다르게 Queue는 Head와 Tail 두개가 필요하다. 앞서 다룬 stack보다 좀더 생각할 거리가 늘어나게 된다.
만약 새 값이 insert 될때 Tail과 Head는 어떻게 될까? head는 그대로 있고 Tail은 위로 한칸 움직일 것이다.
반대로 값이 delete 되면 Head가 위로 한칸 올라갈것이다.
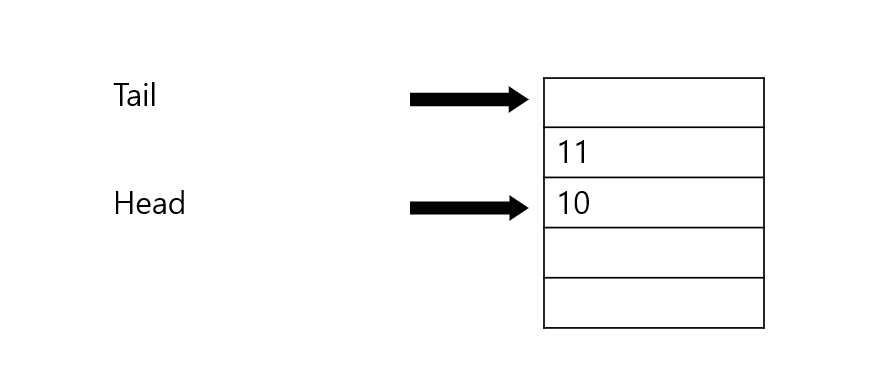
그렇다면 다음과 같은 상황에서 Tail에 새 값이 새로 insert가 되면 어떻게 될까? 간단하다 제일 밑의 빈공간에 Tail이 가리키게 된다. 아래의 그림과 같이 말이다.
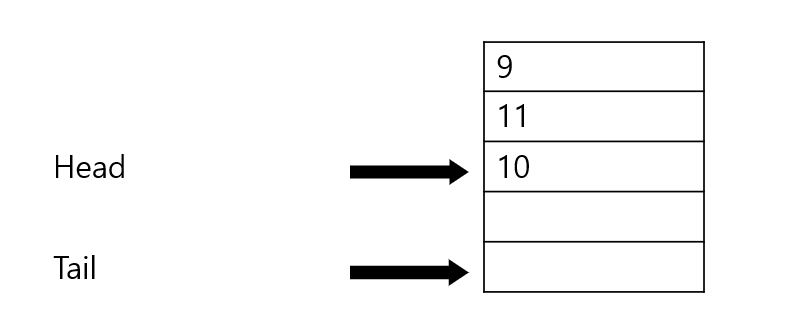
그러면 이 상황에서 좀 더 나아가서 생각해보자. 여기서 값을 꽉차도록 넣으면 다음과 같은 상황이 발생한다.
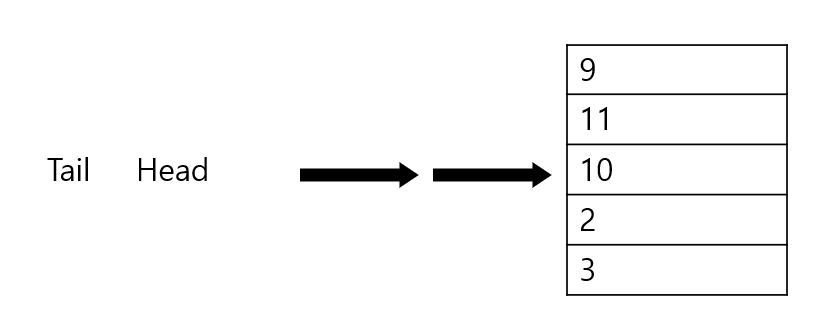
Tail 과 Head가 겹치는 일이 발생한다. 그리고 이 상태에서 값을 하나씩 제거 한다고 해보자 하나씩 제거해 가다보면
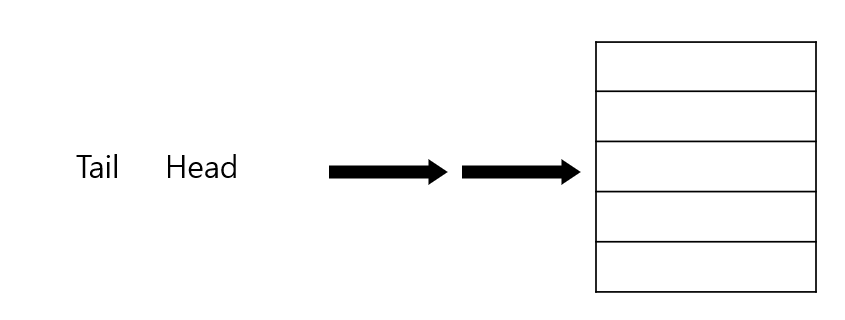
결과 적으로 이렇게 될 것이다. 뭔가 이상함을 느끼지 않았는가 ? 그렇다 Tail과 Head로 꽉차 있을 때랑 비어있을 때 구별을 할 수 없게 된다. 이것은 Queue에서 오래된 이슈이며 이것을 해결하는 방법 또한 간단한 편이다.
해결방법은 꽉 차기전에 값을 받지 않게 만들면 된다.
Queue Code
int Queue[N];
int Head, Tail;
int init() {
Head = 0;
Tail = 0;
}
int isEmpty() { return Head == Tail ; }
int insert(int x) {
Queue[Tail] = x;
Tail ++;
Tail = Tail % N;
}
int delete(){
int oldHead = Head;
Head++; Head = Head % N ;
return Queue[oldHead];
}간단하게 Stack과 Queue에 대해 알아보았다. 이제 스택과 큐로 무엇을 활용할 수 있는지 다음 포스팅에서 알아보도록 하겠다.
# 미로찾기
미로찾기 문제를 Queue를 이용해서 푸는 방법을 알아보겠다.
Map 하고 i,j는 지난번 방법과 같다.
다만 지난번 방법하고 다르게 가까운데를 먼저 가보게끔 구현을 하게된다.
이러한 BFS 의 특징중에 하나는 제일 짧은 길을 찾을 수 있다는 것이다.
코드는 다음과 같은 형식을 가지게 된다.
BFS 명시적 Queue
int Map[M][N];
int i, j;
int Find()
{
QueueInsert(0, 0);
while(1 ){
if(Map[i][j]=='*'){if(IsEmpty())...
Map[i][j] = '*'; //목적지 확인
if(Map[i-1][j]=='0'){Insert(i-1); Insert(j);} // 8번 확인
if(IsEmpty()) break;
i=pop(); j=pop();
}
}
'학부 내용 정리 > [ 2-1 ] 자료구조' 카테고리의 다른 글
| [ 자료구조 ] Linked List (0) | 2022.06.14 |
|---|---|
| [ 자료구조 ] Equivalence Relation(동치 관계) (0) | 2022.06.14 |
| [ 자료구조 ] Stack (0) | 2022.06.14 |
| [ 자료구조 ] String Matching (Naive , DFA , KMP) (0) | 2022.06.13 |
| [ 자료구조 ] 배열 (Search, Insert, Delete) (0) | 2022.06.13 |