반응형
Stack
- Insert/Delete만 제공
- Push/Pop이라고 부름
- Last in, First out(나중에 들어오는게, 먼저 나가는 것)
- 성능: Push: O(1), Pop: O(1)(넣는것을 push, 빼는것을 pop)
Stack 구현
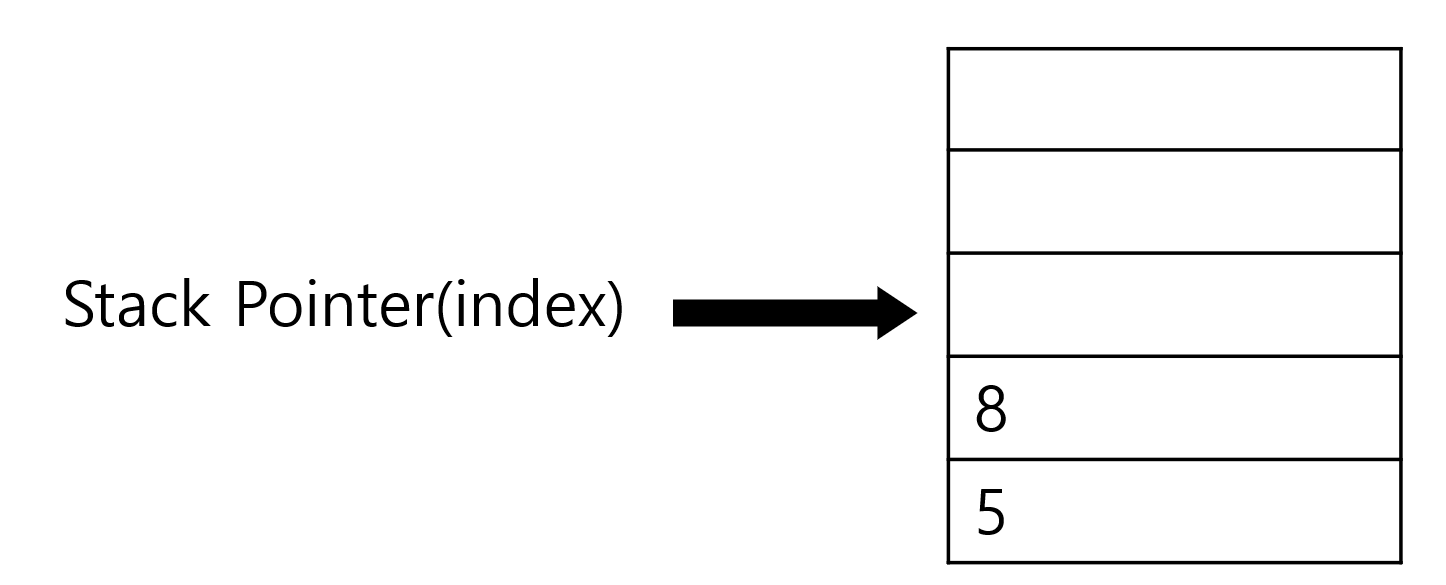
Stack Code
int Stack[N];
int SP;
int init() {SP = 0}
int isEmpty() {return SP == 0;}
int Push()
{
Stack[SP] = x; SP++;
}
int Pop()
{
SP--; return Stack[SP];
}
# 미로찾기
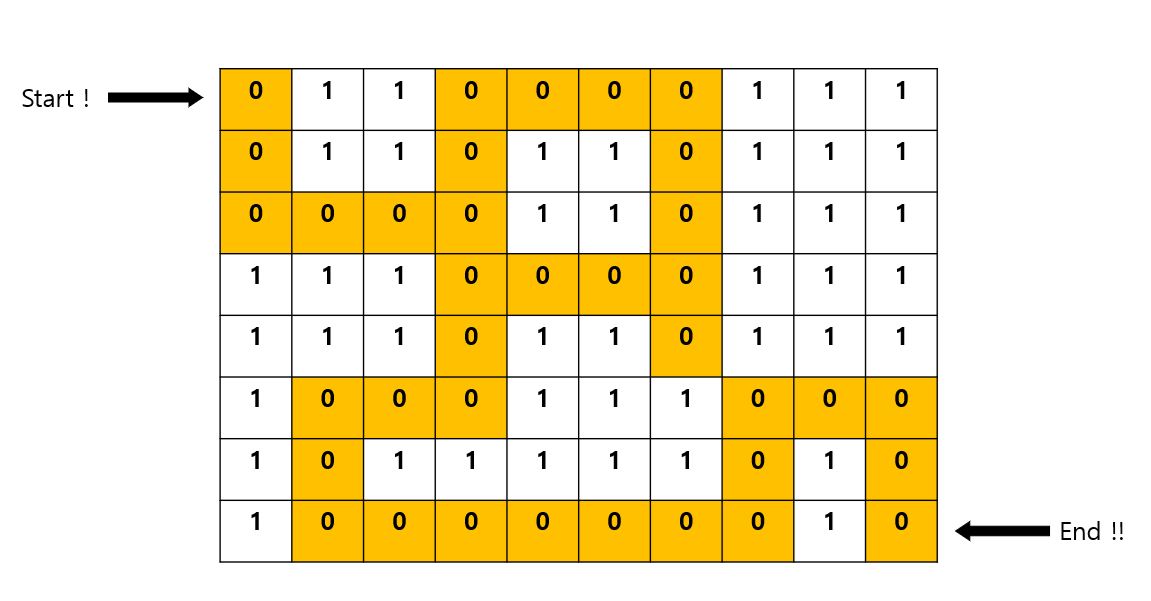
이런 미로 문제를 해결하는 알고리즘 중에 DFS 와 BFS가 있다. 오늘은 DFS로 미로를 찾는 과정을 알아볼것이다.
먼저 미로길을 찾기 위해서는 크게 2가지 Tool이 있어야 한다.
하나는 실을 풀어서 다시 제자리로 돌아올수 있는 Tool, 그래야 막혔을때 다시 뒤로 돌아올수 있기 때문이다.
이것은 Stack 의 구조를 이용해서 좌표들을 저장해놓고 다시 뒤로 스택에서 뽑으면 뒤로 돌아갈수 있게 할수 있다.
그리고 갔던길을 다시 가지 않도록 하는 Tool 이 필요하다.
갔던길에는 0대신 다른 값으로 채워넣으면 되고 나중에 돌아왔을때 다른값으로 채워진 곳은 가지 않도록 하면 된다.
갈때마다 0 대신에 * 표시를 하면서 전진해 나가면 빙글빙글 돌아서 영원히 헤메는 일이 없어질 것이다.
이렇게 크게 두가지 Tool을 이용해서 미로찾기 문제를 해결한다.
그럼 출발점에서 시작해서 어떤 방식으로 길을 찾아가야할까?
일단 매번 갈때마다 주변을 살펴보고 갈수 있는곳이 있으면 그쪽으로 간다. 이동하고 나면 거기서 새로 깨어난다.
DFS 명시적 Stack
int Map[M][N];
int i, j // 현재 위치
int Find()
{
i= j= 0; //start
Mao[i][j] = *;
while(1) { // 반복
if( i == M-1 && j == N-1) return 1; // 목적지 도착!
ip=-100; jp=-100;
if(Map[i-1][j]=='0'){ip=i-1; jp=j} //*8 8면 중 0이 있는가?
if(ip!=-100){
Push(i); Push(j);i=ip;j=jp;Map[i][j]='*';
}else{ //후진
if(isEmpty()) return -1;
Map[i][j]='X'; j=Pop(); i=Pop();
}
}
}
DFS 명시적 Stack 정확성
- (0,0)에서 어떤 위치 (s, t) 로 가는 길이 있다.
- <=> (0,0), (a1,b1), (a2, b2), ..., (s,t)인 좌표 sequence가 있고 인접한 쌍에서는 둘 중 한 숫자만 1이 차이가 난다.
- Map의 모든 좌표에 초기에 0이 적혀 있다.
- 위와 같은 상황에서 알고리즘은 (s,t)를 반드시 방문한다!
DFS 명시적 Stack 성능
- 알고리즘이 진행하는 순서대로 생각하지 말고 한칸에서 일어나는 일들을 따로 생각해보자. 그 일들을 모든 칸에서 더하면 전체 시간이다.
- 특정한 i, j 일때 생각을 해보자. 그때 전진을 할 수도 있고 후진을 할 수있다. 후진을 하고 나면 다시 그 칸에 안오게 된다. 스택에는 같은 좌표가 두번 들어 갈수가 없다. (동일순간의 스택의 값이 여러개일 수 가 없다.) 전진은 최대 4번까지 가능하다.
- 각각 한 칸에서 걸린 시간이 상수 시간이므로 => O(MN)
반응형
'학부 내용 정리 > [ 2-1 ] 자료구조' 카테고리의 다른 글
| [ 자료구조 ] Equivalence Relation(동치 관계) (0) | 2022.06.14 |
|---|---|
| [ 자료구조 ] Queue (0) | 2022.06.14 |
| [ 자료구조 ] String Matching (Naive , DFA , KMP) (0) | 2022.06.13 |
| [ 자료구조 ] 배열 (Search, Insert, Delete) (0) | 2022.06.13 |
| [ 자료구조 ] 배열 (Merge, Recursive Merge Sort) (0) | 2022.06.13 |