1. vector
- Vector: Variable-Size Array(사이즈가 늘어나고 줄어들 수 있는 배열)
- Sorted
- Search: O(log n), Insert: S+ O(n) , Delete: S+ O(n)
- Unsorted
- Search: O(n), Insert: S + O(1), Delete: S + O(1)
2. Dummy Nodes

Standarad Linked List에 대부분 포함되는 구조. 처음에 만들때 노드를 두개 만들고 하나는 마이너스 무한대 하나는 플러스 무한대 값을 집어넣는다. 이 두 값은 실제로 사용하는 값은 아니고, 미리 경계를 정해놓는 것이다. 이렇게 해놓으면 못찾았을때 (실패했을 때), P와 L이 NULL인 경우가 없어지게 된다.
3. Circular List

Circular Queue 등을 만들때 쓰임, 성능이 달라지는 일은 없다. 특이한 상황에서 쓰이는 구조.
4. Doubly Linked List

성능이 달라질수 있음. 양방향으로 연결되어있어서 노드 앞뒤로 갈 수 있는 구조. 성능이 크게 달라지는 일은 없다.
5. Linked Stack
- Push

- Pop

6. Linked Queue

다만 이 구조에서는 Delete는 불가능 하게 된다. (대신 Doubly Linked List 일떄는 가능)
7. More
Free Block List on File Systems
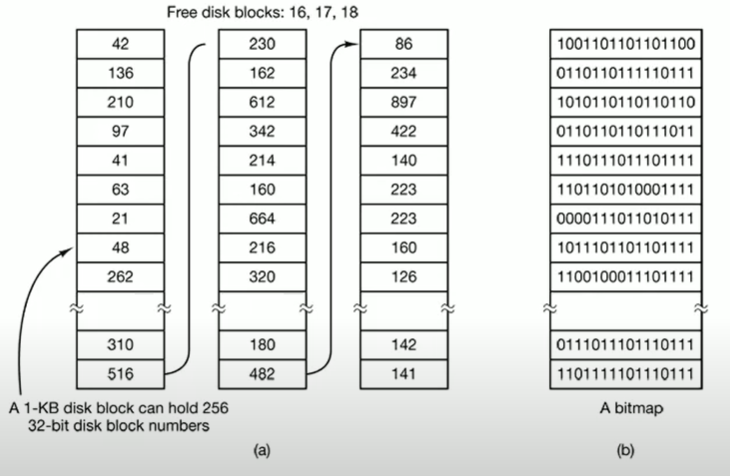
파일 시스템에 쓰이는 링크드 리스트
Polynomial Representation
- Array Version
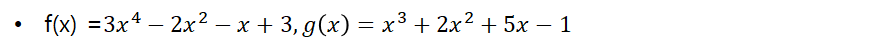
- f(x) + g(x) = ?
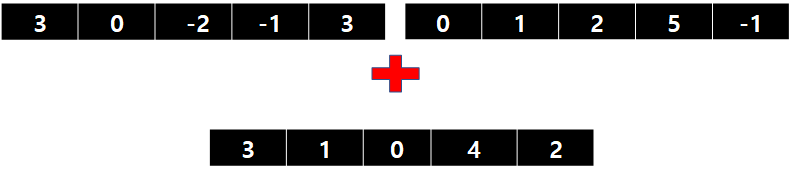
배열에 각 차수의 계수 적어놓기
List Version
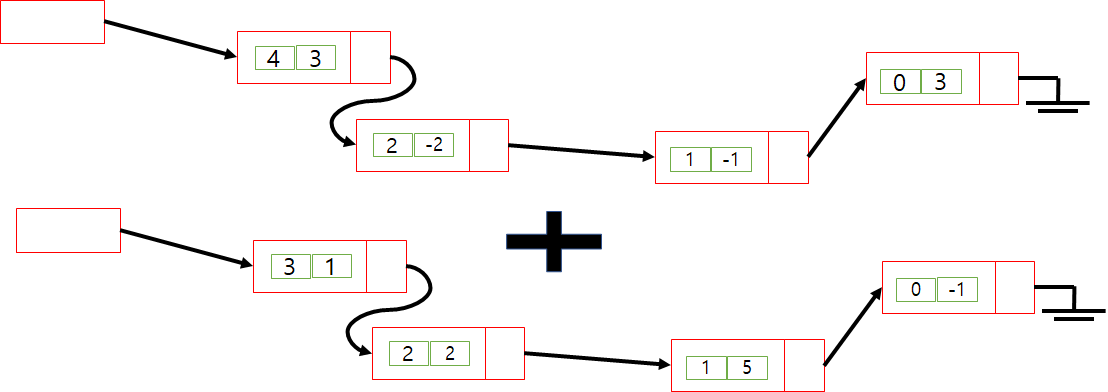
각 노트에 두개의 값이 있다 왼쪽값은 차수 오른쪽 값은 계수이다.
# Result

Sparse Matrix (0의 비율의 많은 Matrix)
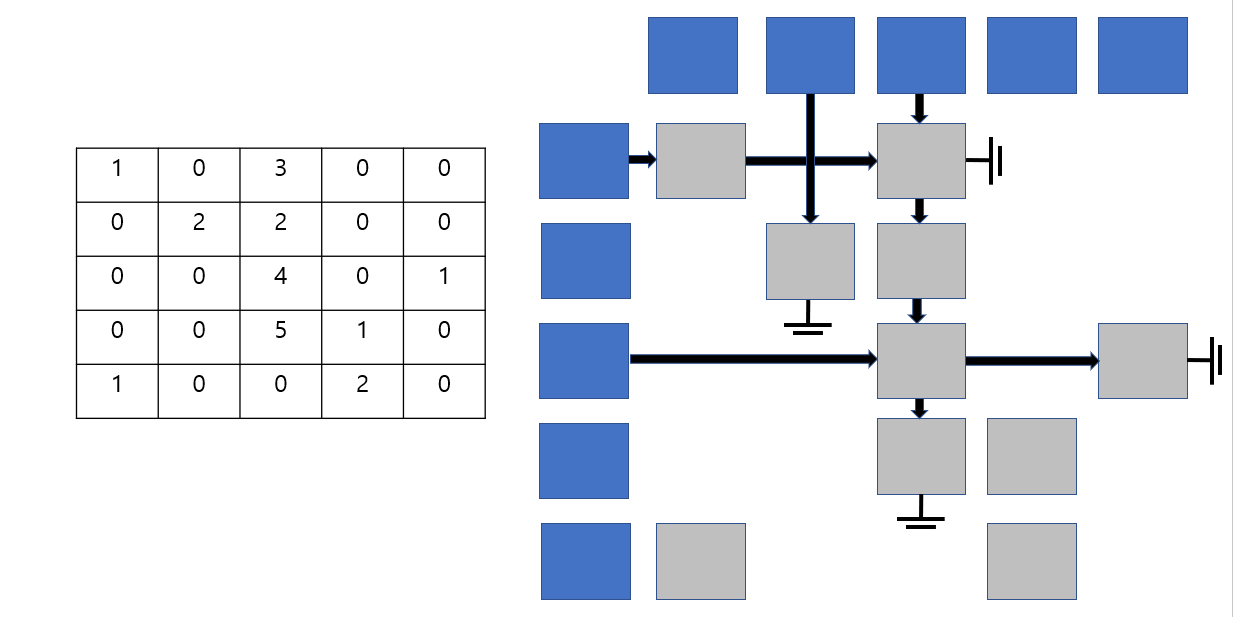
그림과는 다르게 보틍은 doubly linked list로 이를 나타내는것이 편하다.
Sparse Matrix Code
class Node {
int a, r, c;
Node *up, *down, *left, *right; // double linked 가정
}
Sparse Matrix Multiplication( 두 개의 행렬 곱하기 )
행렬의 곱은 부텉 한 행렬의 column 과 다른 행렬의 row의 자리들을 곱하는 형식인데 위의 링크드 리스트를 활용한
matrix에서 두 행렬의 곱셉의 결과를 출력 할 수 있다.
Memory Allocation
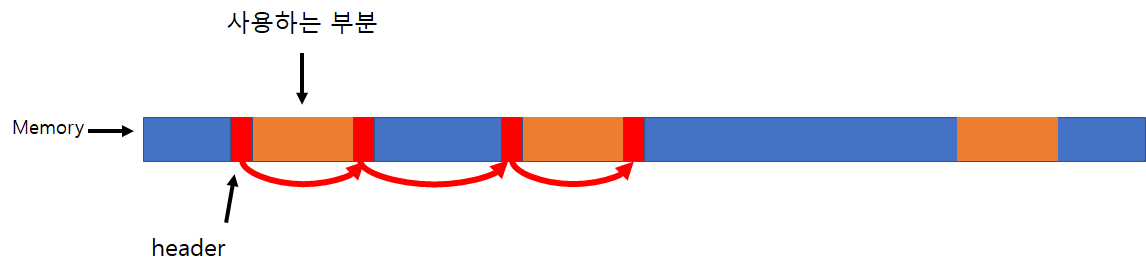
헤더들이 Linked List들로 연결되어 있어서 메모리를 할당 하라는 명령을 받았을때 링크를 따라가면서 적당한 사이즈가 있는지 확인하는 방법으로 활용(물론 매우 거시적으로 설명한뜻 성능 향상을 위해 좀더 복잡한 것들이 쓰임.)
Skip List
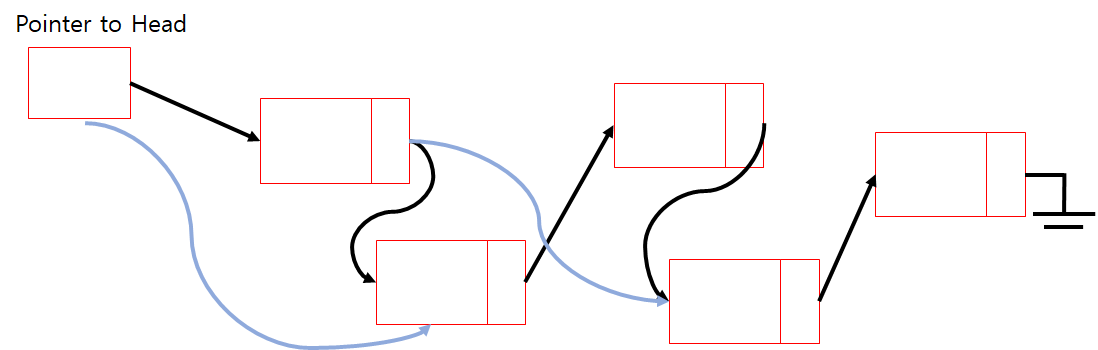
멀리 가는 포인터를 포함해 두면 Linked List로 Binary Search 비슷하게 활용할 수 있다. (멀리 가보고 값을 비교해 보기)
B+ Tree
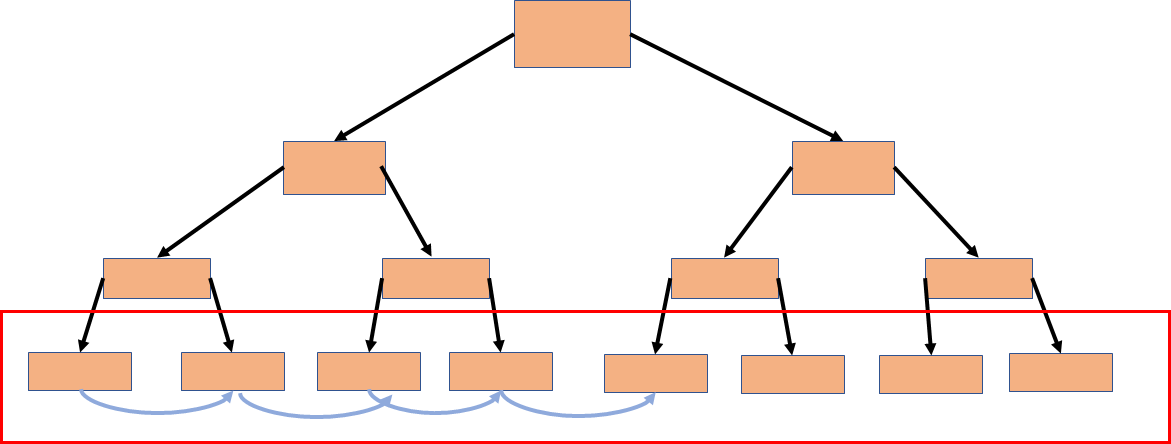
아직 본격적으로 배우지 않았지만 이런 tree 구조(각 노드의 왼쪽에는 노드보다 작은값 오른쪽에는 큰 값을 넣는 구조)에서 가로 방향으로 이동할 수 있게 끔 링크를 줘서 search 작업을 할때 보다 빠르게 수행할 수 있게끔 활용한다.
'학부 내용 정리 > [ 2-1 ] 자료구조' 카테고리의 다른 글
| [ 자료구조 ] Tree (AVL) (0) | 2022.06.14 |
|---|---|
| [ 자료구조 ] Tree (Binary Search Tree) (0) | 2022.06.14 |
| [ 자료구조 ] Linked List (0) | 2022.06.14 |
| [ 자료구조 ] Equivalence Relation(동치 관계) (0) | 2022.06.14 |
| [ 자료구조 ] Queue (0) | 2022.06.14 |