[ 자료구조 ] Tree (Binary Search Tree)

Definition of Binary Search Tree

값은 아무거나 넣을 수 있다. 노드 3개를 묶어서 보았을 때 중간 노드의 값보다 큰 값은 오른쪽 작은 값은 왼쪽으로 들어가게되는 형태이다.

Code for Node

class Node {
    int k;
    Node *l, *r;
    
};​

Search Algorithm

Node *Search(Node *N, int x) 
{
    if (N == Null) return NULL;
    if (N -> k == X) return N;
    else if (N->k < X) return Search(N->r,X)
    else return Search(N->1, X);    
};​

Search Correctness

• To Prove : 만약 x가 노드에 있다면 Search() 는 그 노드를 리턴할 것이고, 아니라면 그것은 실패할 것이다. "
• Proof by cases :
  • Case 1 : Trivial
  • Case 2 : "K < X" 은 X 왼쪽 서브트리에 없다는 것을 의미하고 그것은  X가 왼쪽 서브트리에 있다는 것을 의미한다.
  • Case 3 : Ditto ( Case2 와 대칭 )

Search Performance

Height 에 대해 따로 정의를 안했는데 root에서 마지막 child 노드까지 노드의 개수를 height라고 하겠다. (왼 : height 5 오: height 9)

오른쪽과 왼쪽을 비교해 보았을 때 오른쪽 Tree 는 왼쪽에 비해 노드 개수에 비례한 height가 낮아진다. 직관적으로 생각해보면 Performace 는 height에 비례하게 될 것이다. Tree의 성능은 다음과 같다.

• Given a fixed Tree
  • Worst Case : O(Height)
  • Average Case: ??? (정하기가 매우 곤란함. 논란의 여지가 있음.)
• Considering All Possible Trees
  • Worst Case: O(n)
  • Average Case: Later

Insert

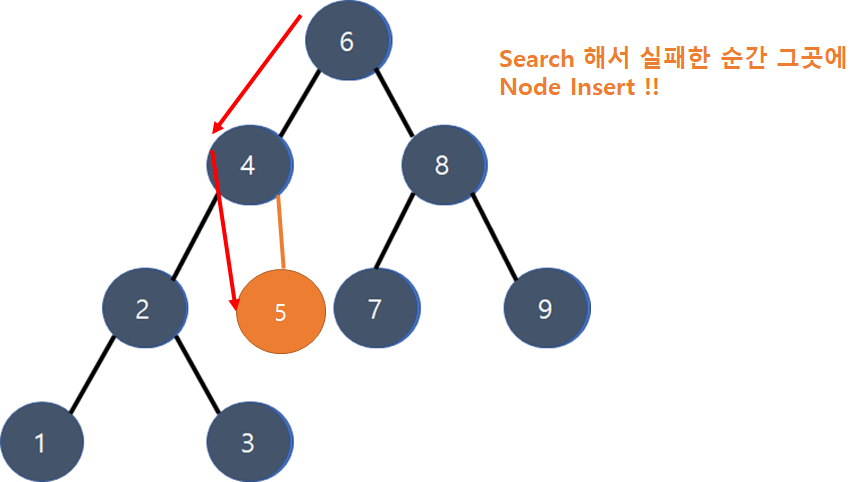
Search를 생각해 봤으니 다음은 Insert를 알아보자. 예를들어서 5를 insert 하려면 어떤 방식으로 넣어야 할까?

Insert Algorithm

• Search가 먼저 선행.
• If Search() succeeds, then Insert() fails. 중복 안됨.
• If Search() fails, 마지막으로 시도했다가 실패한 방향에 삽입

Insert Flow in Tree 

Code for Insert

Node *Insert(Node *N, int X, Node **RP) // 루트, 넣을 값, 넣어진 노트의 부모트리
{
    while ( 1 ) {   
        Node *NN;
        if (N == Null) { //최초에만 발생 가능한 Case
			NN=new node;
            NN->K;
            NN->L=NN->R=NULL;
            *RP=NN;
        } else{
        	if (N->k < X) Insert(N->R, X, &(N->R));
            else if (N->k > X) Insert(N->L, X, &(N->L));
            else retturn NULL;
        }
        
}​

Insert Correctness

• Comes almost directly from the Correctness of Search
• When the algorithm goes down to a SubTree
  • It satisfies the condition that "If X is in the Tree, X is in that SubTree."

Performance

첫번째 case 단순한 루프 ->상수시간이다.
나머지 case들을 봐도 단순히 Search 과정에서 노드를 하나 생성&연결하는 것뿐이므로 결과적으로
Insert 하는데 걸리는 시간은search와 동일하다고 할 수 있겠다.

Delete Algorithm

• search() 먼저 수행하기
• If Search() fails, Delete() also fails
• If Search() succeeds
  • Case 1 : Node has no Child
  • Case 2 : Node has one Child
  • Case 3 : Node has two Children

Case 1 : Node has no Child

• Correctness trivial

예를 들어 child가 하나도 없는 7을 지울 때 간단하게 7만 자르고 8이 적힌 node에 NULL을 가리키게 한다.

child가 없는 노드를 지울 때 아무 문제 없는지 살펴보자. 만약 8번 노드 왼쪽에 subtree 가 있으면 지워져도 그 subtree는 child가 없기때문에 문제가 없다. 왼쪽은 무조건 노드의 작은값이 들어가기 때문에 tree의 구조가 깨질일이 없다.

Assume Dummy Root

코딩 하기 편리하게 Dummy Root를 넣어 두고 가정한다.(이런 식의 Skill은 코딩이 편하게 되는 자주 쓰이는 Skill 중 하나이다.)

Code for Delete Case 1

int Delete(Node *N, Node *P)
{
     if(N->l === NULL && N->r == NULL) {
        if(N == P->l) P-> l = NULL;
        else P->r =NULL;
        delete N;
    }
};​

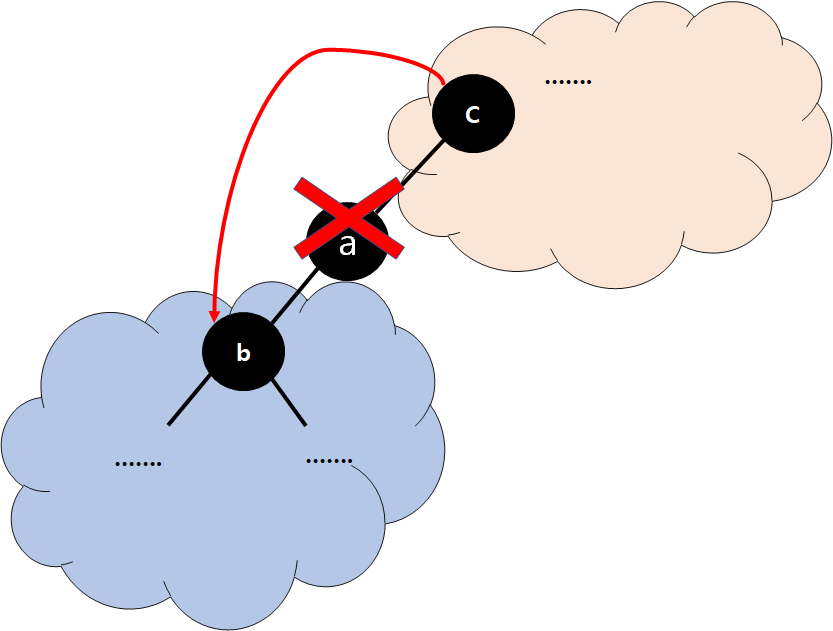
Case 2 : Node has one Child

이러한 case의 tree의 일부분을 생각해본다.

a를 삭제하는 방법은 c에서 바로 b로 가게 만들면 된다.

Case 2 Correctness

• b 아래에 있는것들은 변하지 않는다.
  
  • 파란영역에 있는 노드들은 문제 없다.
• b 아래의 모든 것들은 이미 c의 왼쪽 하위 트리에 있다.
  
  • 따라서 빨간색 영역의 모든 노드가 만족합니다.

Code for Delete Case 2

int Delete(Node *N, Node *P)
{
     else if (N->l != NULL && N->r ==NULL) // N의 왼쪽이 null이 아니고 오른쪽이 null인 경우
    {
        if(N == P ->l){
        	if(N->l!=NULL)P->l = N->l;
            else P-> l = N->r;
        } else{
       		if(N->l!=NULL)P->r = N->l;
            else P-> l = N->r;
        }
    }
};

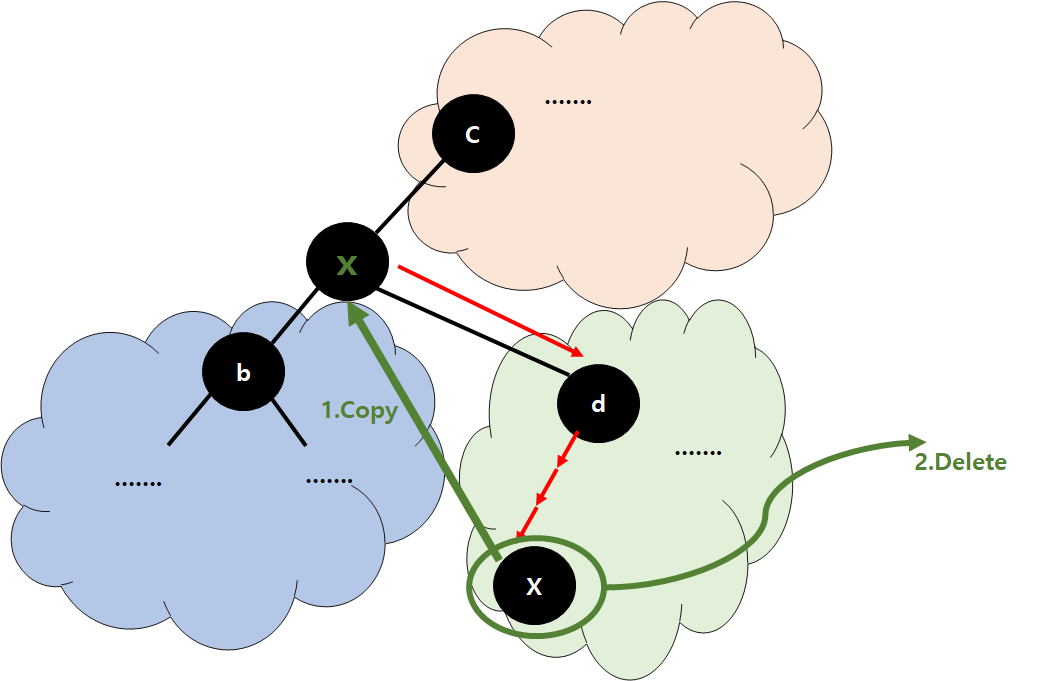
Case 3 Node has two Children

a 노드에 3부분이 연결되어 있는 경우이다. a를 삭제하라면 어떻게 해야할까?

다음과 같이 a에서 오른쪽으로 한번 그다음 계속 왼쪽으로 이동해서 제일 아래 값 x를 찾아 a 자리에 복사 후 x를 지워낸다. 

Case 3 Correctness

• If we sort all keys
  • ...................a,x, ............... (-> tree 모든 node 한줄로 sorting)
  •  x 는 a뒤에 있다.
  • 만약 x를 노드에 a에 대해 놓으면, BST 조건은 원래 x를 제외한 모든 노드에 의해 충족된다(괜찮다).
  • 트리에 a와 x 사이의 값이 없기 때문입니다.

Alternative Proofs

• Lemma : Search()를 성공적으로 한다면 BTS Delete 도 성공적이다. 그 반대도 성립한다.
• Proof
  • Case 1 : BST is correct -> Search() 성공
  • Case 2 : BST is incorrect -> Search() 실패하는 것이 하나라도 있다.

Proof using the Lemma

• Case 1 : Trivial
• Case 2 : 설명필요.
• Case 3 : 설명필요.

• Continuity Lemma Intuition

(왼) BST 구조를 쭉펴서 나열하면 다음과 같은 형태(오)가 될것이다.

Proof

Search Performance

• Given a fixed Tree
  • Worst Case: O (Height)
  • Average Case : There are not many nodes near the top!
• Considering All Possible Trees
  • Worst Case: O(n)
  • Average Case: Consider only insert, values 1,2, ... , n are inserted in random order
  • Random order: all of n! permutations are equally likely
  • Probability that the root has 1 is 1/n, 2 is 1/n, ... , n is 1/n
  • E(Height of n Nodes):
  • 
  • Turns out to be O(log n), also with high probability(대다수의 경우 높은 확률로)